Question 123204: 3x+y<9 , the < or > signs means equal to or greater or lesser than.
x-y<7, the > has a line under it. Didn't know how to make it on here.
x>0,
Which of the following points satisfy the inequalities?
(2,5), ( 0,9), (3,-2) or (-1,0)
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! The best way is to plot these
(1) 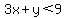
(2) 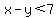
(3) 
----------------
Find  in terms of in terms of 
(1) 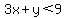
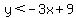
(2) 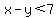

multiply both sides by  and reverse the < sign and reverse the < sign
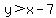
(3) 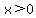 No No  involved here. This is saying that involved here. This is saying that 
can never be  or negative. It's domain is the right half of or negative. It's domain is the right half of
the graph
I'll do a plot of
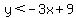 and and
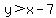

The solution is the little triangular area bounded by the  axis axis
and the lines. Now see which points are in that area
-----------------
(2,5) looks to be just outside, and it fails (1) because
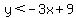
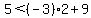
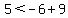
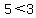 This is clearly not true This is clearly not true
------------------
(0,9) This looks like it might be in the area, but it fails (1) also
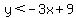
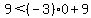
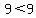 This is clearly not true also This is clearly not true also
------------------
(3,-2) This fails in the area
------------------
(-1,0)  can't be negative, as I said, and it is can't be negative, as I said, and it is
also clearly outside the area
-------------------
So, only (3,-2) satisfies the inequalities answer
|
|
|