Question 122762: Solve.
If a ball thrown vertically upward from a height of 5ft, with an initial velocity of 80 ft/s, it's height(h) after (t) second is given by h=-16t squared + 80t + 5. ow long does it take the ball to return to the ground?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! When the ball hits the ground, this means  (in other words, the height is zero) (in other words, the height is zero)
 Start with the given equation Start with the given equation
 Plug in Plug in  . .
Let's use the quadratic formula to solve for t:
Starting with the general quadratic

the general solution using the quadratic equation is:

So lets solve  ( notice ( notice  , ,  , and , and  ) )
 Plug in a=-16, b=80, and c=5 Plug in a=-16, b=80, and c=5
 Square 80 to get 6400 Square 80 to get 6400
 Multiply Multiply 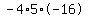 to get to get 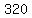
 Combine like terms in the radicand (everything under the square root) Combine like terms in the radicand (everything under the square root)
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Multiply 2 and -16 to get -32 Multiply 2 and -16 to get -32
So now the expression breaks down into two parts
 or or 
Now break up the fraction
 or or 
Simplify
 or or 
So these expressions approximate to
 or or 
So our possible solutions are:
 or or 
However, since a negative time doesn't make sense, our only solution is

-----------------------------
Answer:
So at around 5.06 seconds, the ball will hit the ground.
|
|
|