Question 122759: Solve.
(1)x squared - 7x - 1 = 0
(2)x squared - 4x - 4 = 0
(3)6x squared = 9x
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! # 1
Let's use the quadratic formula to solve for x:
Starting with the general quadratic

the general solution using the quadratic equation is:

So lets solve  ( notice ( notice  , ,  , and , and  ) )
 Plug in a=1, b=-7, and c=-1 Plug in a=1, b=-7, and c=-1
 Negate -7 to get 7 Negate -7 to get 7
 Square -7 to get 49 (note: remember when you square -7, you must square the negative as well. This is because Square -7 to get 49 (note: remember when you square -7, you must square the negative as well. This is because  .) .)
 Multiply Multiply  to get to get 
 Combine like terms in the radicand (everything under the square root) Combine like terms in the radicand (everything under the square root)
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Multiply 2 and 1 to get 2 Multiply 2 and 1 to get 2
So now the expression breaks down into two parts
 or or 
Now break up the fraction
 or or 
Simplify
 or or 
So these expressions approximate to
 or or 
So our solutions are:
 or or 
Notice when we graph 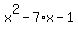 , we get: , we get:

when we use the root finder feature on a calculator, we find that  and and  .So this verifies our answer .So this verifies our answer
# 2
Let's use the quadratic formula to solve for x:
Starting with the general quadratic

the general solution using the quadratic equation is:

So lets solve  ( notice ( notice  , ,  , and , and  ) )
 Plug in a=1, b=-4, and c=-4 Plug in a=1, b=-4, and c=-4
 Negate -4 to get 4 Negate -4 to get 4
 Square -4 to get 16 (note: remember when you square -4, you must square the negative as well. This is because Square -4 to get 16 (note: remember when you square -4, you must square the negative as well. This is because  .) .)
 Multiply Multiply 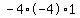 to get to get 
 Combine like terms in the radicand (everything under the square root) Combine like terms in the radicand (everything under the square root)
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Multiply 2 and 1 to get 2 Multiply 2 and 1 to get 2
So now the expression breaks down into two parts
 or or 
Now break up the fraction
 or or 
Simplify
 or or 
So these expressions approximate to
 or or 
So our solutions are:
 or or 
Notice when we graph 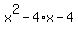 , we get: , we get:

when we use the root finder feature on a calculator, we find that  and and  .So this verifies our answer .So this verifies our answer
# 3
 Start with the given equation Start with the given equation
 Subtract 9x from both sides Subtract 9x from both sides
 Factor the left side Factor the left side
Now set each factor equal to zero:
 or or 
 or or  Now solve for x in each case Now solve for x in each case
So our answer is
 or or 
Notice if we graph  we can see that the roots are we can see that the roots are  and and  . So this visually verifies our answer. . So this visually verifies our answer.

|
|
|