Question 12254: hello mam\sir i have some doubts in following questions
1.find the cube root of 3+isquare root 3
2.if z=x+iy ,proove that |x|+|y|less than or equal to sqareroot2|z|
3.proove [ a+b omega+c(omega)^2] divided by [a omega+b (omega)^2+c]=(omega)^2
4.proove 1+(omega)^n+(omega)^2n=0 when n=2,4
thank you in advance
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.find the cube root of 3+isquare root 3
Do you mean cubic root of(3 + i sqrt(3)) I guess do.
To solve: 
Since 
where r = sqrt(3^2+ 3) = 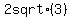
 , i.e. w = pi/6. , i.e. w = pi/6.
By De Mieve theorem,  ,k = 0,1,2 ,k = 0,1,2
Hence, 

or 

or 

2.if z=x+iy ,prove that |x|+|y| less than or equal to sqareroot(2)|z|
proof: Since 
and 
Consider 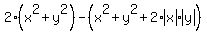
= 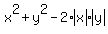
= 
Hence, 
By taking sqrt, we have 
**You should define what w (omega) is, I guess, it is

3.prove [ a+b omega+c(omega)^2] divided by [a omega+b (omega)^2+c]=(omega)^2
Proof: 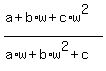
= 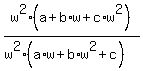
= 
[ Since  , ,  ] ]
= 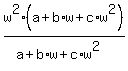
=  [ [ 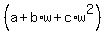 is cancelled ] is cancelled ]
4.prove 1+(omega)^n+(omega)^2n=0 when n=2,4
Proof: Since 
= 
= 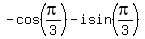
and 
= 
= 
When n =2, 
[Note:  ] ]
= 
= 
{or use ew is the primitive root of  directly] directly]
Similarly, when n =4, 
[Note:  ] ]
Kenny
|
|
|