SOLUTION: Find all real or imaginary solution to the question. 6x=-(19x+25)/x+1

I'm going to assume you meant







rather than









First make a note to exclude  if it happens to come up as a potential root of the equation because -1 is not in the domain of the right hand side of the equation because -1 would make the denominator equal zero.





Second, move everything to the left of the equal sign, thus:









 is your common denominator, so:











Simplify the numerator









Remember that  if and only if  and 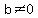, meaning that we need to solve for:











Oddly enough, this mess actually factors.





, hence











or











Since neither of these roots = -1, both are valid potential roots of the

equation.  However, since we introduced an  term by applying the

common denominator, we need to check both roots against the possiblity that

one of them is extraneous.













  First root checks.













  Second root checks.





Done