Question 122231: if i have a parametric matrix and i want to find parametric Eigenvectors and Eigenvalues....what i have to do??? and these Eigenvectors and Eigenvalues are still parametric or i have to equal them????
thanx
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! Although it's difficult to give a general answer, here goes.
You do it the same way you solve an eigenvalue/eigenvector problem for a regular (non-parametric) matrix.
Let's use an example.
Let A be your 2x2 parametric matrix,
where s is your parameter.
First, set up your eigenvalue problem,
I'm using 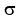 instead of lambda, the traditional eigenvalue Greek symbol, here.
Find your characteristic polynomial,
Now it gets tricky.
As you can see from the solution for 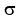, the parameter(s) position(s) in the parametric matrix determines what effect it has on the characteristic polynomial.
In this example, depending on whether s is positive or negative, could lead to real or complex roots.
Once you have the eigenvalues, you would go back to your matrix,
The solution vectors ( , ) are the eigenvectors tied to each of the specific eigenvalues .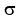
The parameter information is included through the characteristic polynomial for the eigenvalue and the matrix for the eigenvector.
Hope it helps!
|
|
|
