SOLUTION: If I increase my usual driving speed by 10 km/h, I can drive the 255 km trip to Nashville in 24 min less than usual. How fast do I usually drive? PLEASE HELP!!!! There is not an an

Algebra ->  Numeric Fractions Calculators, Lesson and Practice -> SOLUTION: If I increase my usual driving speed by 10 km/h, I can drive the 255 km trip to Nashville in 24 min less than usual. How fast do I usually drive? PLEASE HELP!!!! There is not an an      Log On


   

Question 122155This question is from textbook algebra: structure and Method: book 1
: If I increase my usual driving speed by 10 km/h, I can drive the 255 km trip to Nashville in 24 min less than usual. How fast do I usually drive? PLEASE HELP!!!! There is not an answer in the back, and I also don't know what to do!!!!HELP!!!!!!!!!!!!!!!!!!! I am sorry if this is not enough info, but that is all there is in the book. This question is from textbook algebra: structure and Method: book 1

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!

First note that 24 minutes is 0.4 hour.


Next, we know that the distance from home to Nashville doesn't change, so
if the speed you generally travel is r, and we know that d=rt, we can say
that rt=255.

We also know that 10 km/hr faster gets us there 0.4 hour sooner, so

%28r%2B10%29%28t-0.4%29=255


r=255%2Ft and
r%2B10=255%2F%28t-0.4%29 => r=%28255%2F%28t-0.4%29%29-10


Therefore 255%2Ft=%28255%2F%28t-0.4%29%29-10


Put everything on the left:
255%2Ft-%28255%2F%28t-0.4%29%29%2B10=0


Find the LCD.  Factors are t, (t-0.4), and 1.  So the LCD is t(t-0.4).
Don't bother to multiply it out.  That won't help at this point.


Convert the three fractions to have the LCD:
%28255%28t-0.4%29-255t%2B10t%28t-0.4%29%29%2Ft%28t-0.4%29=0


Simplify the numerator
%28255t-102-255t%2B10t%5E2-4t%29%2Ft%28t-0.4%29=0
%2810t%5E2-4t-102%29%2Ft%28t-0.4%29=0


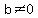Since a%2Fb=0 if and only if a=0 and b%3C%3E0, we only have to
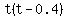solve for 10t%5E2-4t-102=0 and exclude any roots that make t%28t-0.4%29
equal zero because you can't divide by zero.


I'll let you handle the work of solving the quadratic, but suffice it to say
that the roots are 3.4 and -3.  Since we are solving for time, -3 can be
excluded.  As much as we would like to be able to turn back the clock, negative
time just doesn't make much sense.


Knowing that the normal time it takes to get there is 3.4 hours, you can easily
calculate your normal rate, r=255%2F3.4=75  So your normal rate is 75 km/hr.

Just under 47 mph -- slowpoke!