|
Question 122099: What is the radius and center of a circle with the equation x^2+y^2=100?
What is the radius and center of a circle with the equation (x-4)^2+y^2=25?
What is the radius and center of a circle with the equation (x+5)^2+(y-3)^2=18?
What is the radius and center of a circle with the equation x^2+y^2+4*x-2*y=4?
What is the radius and center of a circle with the equation x^2+y^2=2*x+10*y+25=0?
Found 2 solutions by Fombitz, solver91311:
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! The general equation for a circle with center (h,k) and radius, r, is,

What is the radius and center of a circle with the equation  ? ?
Compare the terms to the general equation.






The center is( , , ), radius ), radius 
What is the radius and center of a circle with the equation  ? ?
The center is( , , ), radius ), radius 
What is the radius and center of a circle with the equation  ? ?
The center is( , , ), radius ), radius 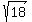
The next two require you to "complete the square" in both x and y and then compare it to the general form.
What is the radius and center of a circle with the equation  ? ?




The center is( , , ), radius ), radius 
What is the radius and center of a circle with the equation 



The center is( , , ), radius ), radius 
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The equation of a circle with center at (h,k) and radius r is:

In your first example, you could re-write the equation as

Therefore h = 0 and k = 0 so the center is at (0,0) and the radius is 10
The second example is a trivial application of what I just showed you,
so you can do that one yourself.
The third one has the slight twist that  , so , so 
The fourth one is a bit trickier. You need to complete the square for each of the variables

First rearrange:

Now, what constant, p, do you need to add so that 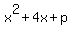 is a perfect is a perfect
square? Let's try 4.  . So add 4 to both sides of . So add 4 to both sides of
the equation.

Next, look at the y terms. If we add 1,  , so add 1 to , so add 1 to
both sides of the equation.

Collect terms on the right, and factor the x and y parts of the left

Remember the minus signs in the standard circle equation, 
That means we need to re-write the x part:

Now we have the circle's parameters directly: Center at (-2,1), radius = 3
Using the process I just showed you for the fourth example, you should be able
to solve the fifth one as soon as you determine whether the equal sign between
the  and and  terms should be a plus sign or a minus sign. terms should be a plus sign or a minus sign.
(Did you hit the adjacent key or forget to shift?)
Hope that helps,
John
|
|
|
| |