SOLUTION: What is the radius and center of a circle with the equation x^2+y^2=100? What is the radius and center of a circle with the equation (x-4)^2+y^2=25? What is the radius and center

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: What is the radius and center of a circle with the equation x^2+y^2=100? What is the radius and center of a circle with the equation (x-4)^2+y^2=25? What is the radius and center      Log On


   

Question 122099: What is the radius and center of a circle with the equation x^2+y^2=100?
What is the radius and center of a circle with the equation (x-4)^2+y^2=25?
What is the radius and center of a circle with the equation (x+5)^2+(y-3)^2=18?
What is the radius and center of a circle with the equation x^2+y^2+4*x-2*y=4?
What is the radius and center of a circle with the equation x^2+y^2=2*x+10*y+25=0?
Found 2 solutions by Fombitz, solver91311:
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
The general equation for a circle with center (h,k) and radius, r, is,
%28x-h%29%5E2%2B%28y-k%29%5E2=r%5E2
What is the radius and center of a circle with the equation x%5E2%2By%5E2=100?
Compare the terms to the general equation.
%28x-h%29%5E2=x%5E2
h=0
%28y-k%29%5E2=y%5E2
k=0
r%5E2=100
r=10
The center is(0,0), radius 10
What is the radius and center of a circle with the equation %28x-4%29%5E2%2By%5E2=25?
The center is(4,0), radius 5
What is the radius and center of a circle with the equation %28x%2B5%29%5E2%2B%28y-3%29%5E2=18?
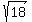
The center is(-5,3), radius sqrt%2818%29
The next two require you to "complete the square" in both x and y and then compare it to the general form.
What is the radius and center of a circle with the equation x%5E2%2By%5E2%2B4%2Ax-2%2Ay=4?
x%5E2%2By%5E2%2B4x-2y=4
x%5E2%2B4x%2By%5E2-2y=4
%28x%5E2%2B4x%2B4%29%2B%28y%5E2-2y%2B1%29=4%2B4%2B1
%28x%2B2%29%5E2%2B%28y-1%29%5E2=9
The center is(-2,1), radius 3
What is the radius and center of a circle with the equation x%5E2%2By%5E2=2x%2B10y%2B25=0
x%5E2-2x%2By%5E2-10y=25
%28x%5E2-2x%2B1%29%2B%28y%5E2-10y%2B25%29=25%2B1%2B25
%28x-1%29%5E2%2B%28y-5%29%5E2=51
The center is(1,5), radius sqrt%2851%29

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


The equation of a circle with center at (h,k) and radius r is:





%28x-h%29%5E2%2B%28y-k%29%5E2=r%5E2





In your first example, you could re-write the equation as





%28x-0%29%5E2%2B%28y-0%29%5E2=10%5E2





Therefore h = 0 and k = 0 so the center is at (0,0) and the radius is 10





The second example is a trivial application of what I just showed you,

so you can do that one yourself.





The third one has the slight twist that r%5E2=18, so r=sqrt%2818%29=3%2Asqrt%282%29





The fourth one is a bit trickier.  You need to complete the square for each of the variables





x%5E2%2By%5E2%2B4%2Ax-2%2Ay=4





First rearrange:





x%5E2%2B4x%2By%5E2-2y=4





Now, what constant, p, do you need to add so that 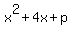x%5E2%2B4x%2Bp is a perfect

square?  Let's try 4.  x%5E2%2B4x%2B4=%28x%2B2%29%5E2.  So add 4 to both sides of

the equation.





x%5E2%2B4x%2B4%2By%5E2-2y=4%2B4





Next, look at the y terms.  If we add 1, y%5E2-2y%2B1=%28y-1%29%5E2, so add 1 to

both sides of the equation.





x%5E2%2B4x%2B4%2By%5E2-2y%2B1=4%2B4%2B1





Collect terms on the right, and factor the x and y parts of the left





%28x%2B2%29%5E2%2B%28y-1%29%5E2=9





Remember the minus signs in the standard circle equation, %28x-h%29%5E2%2B%28y-k%29%5E2=r%5E2

That means we need to re-write the x part:





%28x-%28-2%29%29%5E2%2B%28y-1%29%5E2=3%5E2





Now we have the circle's parameters directly:  Center at (-2,1), radius = 3





Using the process I just showed you for the fourth example, you should be able

to solve the fifth one as soon as you determine whether the equal sign between

the y%5E2 and 2x terms should be a plus sign or a minus sign.



(Did you hit the adjacent key or forget to shift?)





Hope that helps,

John