|
Question 121973: 1) Glenn can paint a house in 9 hours while Stewart can paint the same house in 16 hours.They work together for 4 hours.After 4 hours,Stewart left and Glenn finished the job alone.How many more hours did it take Glenn to finish the job?
2)It takes Butch twice as long as it takes Dan to do a certain piece of work.Working together they can do the work in 6 days.How long would it take Dan to do it alone?
3)A and B working together can finish painting a house in 6 days.A working alone can finish it in 5 days less than B.How long will it take each of them to finish the work alone?
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!
Glenn can paint a house in 9 hours while Stewart can paint the same house
in 16 hours.They work together for 4 hours.After 4 hours,Stewart left and
Glenn finished the job alone.How many more hours did it take Glenn to
finish the job?
Ther are four painting siruations mentioned in the problem. So we make
this chart: (Note that the "fraction" of the house painted may actually
be 1 whole house painted)
Fraction Rate in Time
of house house/hr.
painted
G. painting 1 house
S. painting 1 house
G. and S. painting for 4 hrs together
G. finishing painting the house
-----------------------------------------------------------------------
The question is:
>>...How many more hours did it take Glenn to finish the job?...<<
So let the answer be x, and write x in the chart as the time for
G. to finish painting the house.
Fraction Rate in Time
of house house/hr.
painted
G. painting 1 house
S. painting 1 house
G. and S. painting for 4 hrs together
G. finishing painting the house x
----------------------------------------------------------------------
Now we read:
>>..Glenn can paint a house in 9 hours while Stewart can paint the same house in 16 hours...<<
That's 1 house in 9 hours that G. can paint, so fill in 1 for the "fraction"
of a house painted and 9 for his time. That's also 1 house in 16 hours that
S. can paint, so fill in 1 for the "fraction" of a house painted and 16 for his
time.
Fraction Rate in Time
of house house/hr.
painted
G. painting 1 house 1 9
S. painting 1 house 1 16
G. and S. painting for 4 hrs together
G. finishing painting the house x
----------------------------------------------------------------------
>>...They work together for 4 hours. After 4 hours, Stewart left...<<
So fill in 4 for the time G. and S. worked together.
Fraction Rate in Time
of house house/hr.
painted
G. painting 1 house 1 9
S. painting 1 house 1 16
G. and S. painting for 4 hrs together 4
G. finishing painting the house x
----------------------------------------------------------------------
Now we fill in G.'s and S,'s rates in houses/hr. by the
Fraction Rate in Time
of house house/hr.
painted
G. painting 1 house 1 1/9 9
S. painting 1 house 1 1/16 16
G. and S. painting for 4 hrs together 4
G. finishing painting the house x
----------------------------------------------------------------------
Now that we know G.'s rate is 1/9, we can fill that in also for his
rate when he is finishing painting the house alone after S. leaves.
Fraction Rate in Time
of house house/hr.
painted
G. painting 1 house 1 1/9 9
S. painting 1 house 1 1/16 16
G. and S. painting for 4 hrs together 4
G. finishing painting the house 1/9 x
----------------------------------------------------------------------
Now to get G. and S.'s combined rate for when they worked together,
we add their respective rates:
and fill that in for the rate when they worked together for 4 hours:
Fraction Rate in Time
of house house/hr.
painted
G. painting 1 house 1 1/9 9
S. painting 1 house 1 1/16 16
G. and S. painting for 4 hrs together 25/144 4
G. finishing painting the house 1/9 x
----------------------------------------------------------------------
Now we fill in the fraction of the house G. and S. painted for the four
hours they worked together by using the formula:
We also use that same formula to fill in the fraction of the house
G. painted while working alone after S. left:
Fraction Rate in Time
of house house/hr.
painted
G. painting 1 house 1 1/9 9
S. painting 1 house 1 1/16 16
G. and S. painting for 4 hrs together 25/36 25/144 4
G. finishing painting the house x/9 1/9 x
----------------------------------------------------------------------
Now we know that the fraction of the house that G. and S. painted
while working together PLUS the fraction of a house that G. painted
after S left must equal to 1 whole house painted, so we have the
equation:
 +  = 
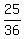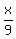Can you solve that by first multiplying thru by LCD of 144? If
not, post again asking how.
Answer: x = 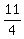 or   or 2 hours 45 minutes.
----------------------------------------------------------------------
----------------------------------------------------------------------
----------------------------------------------------------------------
2)It takes Butch twice as long as it takes Dan to do a certain piece of
work. Working together they can do the work in 6 days. How long would
it take Dan to do it alone?
Make this chart. (Note that the "fraction" of a job may actually
be 1 whole job)
"Fraction" Rate in Time
of job jobs/day
done
Butch alone
Dan alone
Butch and Dan together
------------------------------------------------------
The question is:
>>...How long would it take Dan to do it alone?...<<
So let x = how long it would take Dan to do the job alone.
So fill in x for Dan's time alone, and 1 for the fraction
of a job he does in those x hours.
"Fraction" Rate in Time
of job jobs/day
done
Butch alone
Dan alone 1 x
Butch and Dan together
------------------------------------------------------
>>...It takes Butch twice as long as it takes Dan...<<
So we multiply Dan's time, x, by 2 and fill in 2x for
Butch's time and 1 for the fraction of a job he does:
"Fraction" Rate in Time
of job jobs/day
done
Butch alone 1 2x
Dan alone 1 x
Butch and Dan together
------------------------------------------------------
>>...Working together they can do the work in 6 days...<<
So we fill in 6 for their time working together, and
1 for the fraction of the job done in those 6 days.
"Fraction" Rate in Time
of job jobs/day
done
Butch alone 1 2x
Dan alone 1 x
Butch and Dan together 1 6
------------------------------------------------------
Now we fill in the three rates, using this:
Solve that and get x = 9 days
-----------------------------------------------------
-----------------------------------------------------
-----------------------------------------------------
3)A and B working together can finish painting a house in 6 days.
A working alone can finish it in 5 days less than B.
How long will it take each of them to finish the work alone?
Make this chart, and fill it in. I won't go thru the details
of filling it in as I did above. See if you can look at the
other two problems above and figure out how I filled in the
chart:
"Fraction" Rate in Time
of house house/day
painted
A alone 1 1/(x-5) x-5
B alone 1 1/x x
A and B together 1 1/6 6
I get the equation by
A's rate + B's rate = their combined rate
1 1 1
----- + --- = ---
x-5 x 6
Solve that and get two answers for B's time alone,
x = 2 days and x = 15 days.
Then since A's time is x-5
A's time is 2-5 or -3 days if B's time is 2 days, so we must
discard the answer x = 2, since A's time cannot be negative.
So x = 15 and so B's time can only be 15 days.
Then A's time is x-5 or 15-5 or 10 days.
Edwin
|
|
|
| |
