SOLUTION: Comparing Areas: A wire 360 inches long is cut into two pieces. One piece is formed into a square and the other into a circle. If the two figures have the same area, what are th

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Comparing Areas: A wire 360 inches long is cut into two pieces. One piece is formed into a square and the other into a circle. If the two figures have the same area, what are th      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 121910This question is from textbook College Algebra
: Comparing Areas: A wire 360 inches long is cut into two pieces. One piece is formed into a square and the other into a circle. If the two figures have the same area, what are the lengths of the two pieces of wire (to the nearest tenth of an inch)?
I'm at a lost as to what to do here! I appreciate your help. This question is from textbook College Algebra

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Here's the solution to the same problem except that the overall length of the wire was different. I'll let you go through and change the numbers, but this should help you solve your problem.

==================================================

Let's say the wire is cut into two pieces, one of them is L inches, and the other is 220 - L inches.

If we take the first piece and form it into a square, each one of the sides of the square will be L%2F4 inches, so the area of the square will be A%5Bs%5D=%28L%2F4%29%5E2

The area of a circle is given by A%5Bc%5D=pi%2Ar%5E2, but since the circumference of a circle is given by C=2%2Api%2Ar we can say that the radius of a circle with circumference C is r=C%2F%282%2Api%29.

Now we can re-write the circle area formula as A%5Bc%5D=pi%2A%28C%2F%282%2Api%29%29%5E2, then simplify to:

A%5Bc%5D=C%5E2%2F%284%2Api%29

But we know that A%5Bs%5D=A%5Bc%5D, so:

%28L%2F4%29%5E2=C%5E2%2F%284%2Api%29

L%5E2%2F16=C%5E2%2F%284%2Api%29

Multiply by 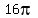16pi

pi%2AL%5E2=4C%5E2

Take the square root

L%2Asqrt%28pi%29=2C

But we know that C=220-L, so substitute:

L%2Asqrt%28pi%29=2%28220-L%29

Distribute and collect like terms:

L%2Asqrt%28pi%29%2B2L=440

Factor out L

L%28sqrt%28pi%29%2B2%29=440

And divide by 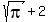sqrt%28pi%29%2B2

green%28L=440%2F%28sqrt%28pi%29%2B2%29%29 inches

C=220-L, so

C=220-%28440%2F%28sqrt%28pi%29%2B2%29%29

Simplify with LCD of 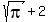sqrt%28pi%29%2B2

C=%28220%28sqrt%28pi%29%2B2%29-440%29%2F%28sqrt%28pi%29%2B2%29

green%28C=220%2Asqrt%28pi%29%2F%28sqrt%28pi%29%2B2%29%29 inches

Check your answer:



. So the areas are equal

Now add the two lengths:
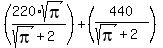
%28220%2Asqrt%28pi%29%2F%28sqrt%28pi%29%2B2%29%29%2B%28440%2F%28sqrt%28pi%29%2B2%29%29

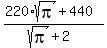
%28220%2Asqrt%28pi%29%2B440%29%2F%28sqrt%28pi%29%2B2%29

%28220%28sqrt%28pi%29%2B2%29%29%2F%28sqrt%28pi%29%2B2%29=220, so the two lengths add to 220.

Answer checks.

Final note: the expressions for L and C developed above are the exact answers. If you want to use a calculator to develop a decimal approximation of the answer, remember that you should never express an answer based on calculations involving measurements to greater precision than the least precise measurement given. Since the length of the wire was expressed to the nearest inch, you should express your answer to the nearest inch as well.