SOLUTION: Dale hikes 15km up a mountain trail. Her return trip on the same trail takes 30 mins less because she is able to increase her speed by 1 km/h. How long does it take her to climb up

Algebra ->  Numeric Fractions Calculators, Lesson and Practice -> SOLUTION: Dale hikes 15km up a mountain trail. Her return trip on the same trail takes 30 mins less because she is able to increase her speed by 1 km/h. How long does it take her to climb up      Log On


   

Question 121905This question is from textbook Algebra: structure and method: Book 1
: Dale hikes 15km up a mountain trail. Her return trip on the same trail takes 30 mins less because she is able to increase her speed by 1 km/h. How long does it take her to climb up and down the mountain? I REALLY NEED HELP WITH THIS!!! The answer is 5 1/2 hours, but I do not know how to get there. I am also supposed to make a chart, but I think I can do that with the info you give me. This question is from textbook Algebra: structure and method: Book 1

Found 2 solutions by stanbon, solver91311:
Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
Dale hikes 15km up a mountain trail. Her return trip on the same trail takes 30 mins less because she is able to increase her speed by 1 km/h. How long does it take her to climb up and down the mountain?
-------------
Up mountain DATA:
Distance = 15 km ; time = x hrs. ; rate = d/t = 15/x km/h
----------------------
Down mountain DATA:
Distance = 15 km ; time = x-0.5 hrs ; rate = 15/(x+0.5) km/h
------------------------
EQUATION:
rate up - rate down = 1 km/h
15/x + 15/(x-0.5) = 1
1/x + 1/(x-0.5) = 1/15
(2x-0.5)/[x(x-0.5)] = 1/15
Cross-multiply to get:
30x - 7.5 = x^2-0.5x
x^2-0.5x+7.5 = 0
2x^2-x+15=0
2x^2-6x+5x-15=0
2x(x-3)+5(x-3)=0
(x-3)*(2x+5) = 0
Positive answer:
x = 3 hrs (time up the mountain)
x-0.5 = 2.5 hrs (time down the mountain)
Total time = 5 1/2 hrs.
===============
Cheers,
Stan H.

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Remember the formula, d=rt

The rate going up is then r=15%2Ft and the rate coming down is 1 km/h faster and the time is a half hour less for the same 15 km, so r%2B1=15%2F%28t-0.5%29

Solve the second equation for r by adding -1 to both sides

r=%2815%2F%28t-0.5%29%29-1 giving us a second expression for r in terms of t.

Now since r = r, we can say:

15%2Ft=%2815%2F%28t-0.5%29%29-1

The LCD is 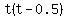t%28t-0.5%29, so



Now put everything on the left:

%2815%28t-0.5%29-%2815t%29%2B%28t%28t-0.5%29%29%29%2Ft%28t-0.5%29=0

Distribute, expand, and collect terms in the numerator but leave the denominator alone:

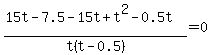
%2815t-7.5-15t%2Bt%5E2-0.5t%29%2Ft%28t-0.5%29=0
%28t%5E2-0.5t-7.5%29%2Ft%28t-0.5%29=0

First consider the zeros of the denominator -- 0 and 0.5. We need to remember these values and exclude them if they come up in the process of finding the zeros of the numerator. For now, just realize that a%2Fb=0 if and only if a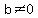=0 and b%3C%3E0. Therefore, all we need to do is solve:

%28t%5E2-0.5t-7.5%29=0

Multiply by 2 to get rid of those pesky decimal fraction coefficients

2t%5E2-t-15=0

Conveniently, this factors:

%282t%2B5%29%28t-3%29=0

So t=3 or t=-2.5. Neither of these values are 0 or 0.5 which would have made the denominator in the original equation go to zero, but we can exclude the negative value. As much as it would be nice to make the clock run backwards sometimes, negative time just doesn't make sense. So, our time up the mountain is 3 hours.

The time down the mountain, is 1/2 hour less, or 2.5 hours. Therefore the total trip was 3 + 2.5 = 5.5 hours.