Question 121745: 1. In this problem, we will analyze the profit found for sales of decorative tiles. A demand equation (sometimes called a demand curve) shows how much money people would pay for a product depending on how much of that product is available on the open market. Often, the demand equation is found empirically (through experiment, or market research).
a. Suppose that a market research company finds that at a price of p = $20, they would sell x = 42 tiles each month. If they lower the price to p = $10, then more people would purchase the tile, and they can expect to sell x = 52 tiles in a month’s time. Find the equation of the line for the demand equation. Write your answer in the form p = mx + b. (Hint: Write an equation using two points in the form (x,p)).
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Note: I'm going to use "y" instead of "p"
Since the price is p=$20, this means y=20 when x=42. So we have the first point (42,20).
Also since the price is p=$10, this means y=10 when x=52. So we have the second point (10,52).
So let's find the equation of the line through the points (42,20) and (10,52):
---------------------
First lets find the slope through the points ( , , ) and ( ) and ( , , ) )
 Start with the slope formula (note: Start with the slope formula (note: ) is the first point ( is the first point ( , , ) and ) and ) is the second point ( is the second point ( , , )) ))
 Plug in Plug in  , , , , , , (these are the coordinates of given points) (these are the coordinates of given points)
 Subtract the terms in the numerator Subtract the terms in the numerator 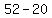 to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 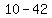 to get to get 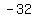
 Reduce Reduce
So the slope is

------------------------------------------------
Now let's use the point-slope formula to find the equation of the line:
------Point-Slope Formula------
 where where  is the slope, and is the slope, and ) is one of the given points is one of the given points
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Distribute Distribute 
 Multiply Multiply  and and  to get to get 
 Add Add  to both sides to isolate y to both sides to isolate y
 Combine like terms Combine like terms  and and  to get to get 
So the equation of the line which goes through the points ( , , ) and ( ) and ( , , ) is: ) is:
 Now replace y with p Now replace y with p
---------------------------------------------------------------
Answer:
So the demand equation is:

|
|
|