|
Question 121474: write an equation of the line that is perpendicular to the line through(9, 10) and (3,-2) and passes through the x intercept of that line?
Found 2 solutions by checkley71, algebrapro18:
Answer by checkley71(8403)   (Show Source):
You can put this solution on YOUR website! find the slope (-2-10)/(3-9)=-12/6=-2 this is the slope
Y=mX+b
10=-2*9+b
b=10+18
b=28 THUS THE EQUATION OF THIS LINE IS:
Y=-2X+28 (RED LINE)
THIS LINE HAS AN X INTERECEPT OF:
0=-2X+28
-2X=-28
X=-28/-2
X=14 OR (14,0)
THE LINE PERPENDICULAR WOULD HAVE A SLOPE=1/2 PASSING THROUGH (12,0)IS:
0=1/2*12+b
b=-6
Y=X/2-6 IS THE EQUATION OF THIS PERPENDICULAR LINE PASSING THROUGH (12,0) OR THE (GREEN LINE)
 (graph 300x300 pixels, x from -6 to 15, y from -10 to 30, of TWO functions y = -2x +28 and y = x/2 -6).
Answer by algebrapro18(249) (Show Source):
You can put this solution on YOUR website! write an equation of the line that is perpendicular to the line through(9, 10) and (3,-2) and passes through the x intercept of that line?
well first off we need to find the equation of the origonal line because we need to find its x-intercept. To do that we first need to find the slop of the line using the following formula:
m =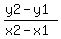 
it doesn't matter what set we choose to be (x1,y1) so I will just choose the first one to make things a little easier.
m = (9-3)/(10--2) <--- Remember minus a negative number is the same thing as +
m = 6/12
m = 1/2
now that we know the slope we can find the equation of the line by applying one of two fomula's, either way you will get the same result. We can use either:
y - y1 = m(x - x1)
OR
y = mx + b and solve for b
using the first formula you get:
y - 10 = 1/2(x - 9)
y - 10 = 1/2x - 9/2
y = 1/2x + 11/2
using the second formula you get:
y = 1/2x+b
10 = 1/2(9) + b
10 = 9/2 + b
11/2 = b
y = 1/2x + 11/2
now we set the above equation equal to 0 and solve for x. This will give us the x-intercept.
1/2x + 11/2 = 0
1/2x = -11/2
x = -11
so the x-intercept of that line is -11.
now we use this infromation to find a line that is perpendicular to the above line and passes though (-11,0).
first off we need to use the fact that perpendicular lines have opposite reciprocal slopes. So the slope of the new line is going to be -2 because the opposite of 1/2 is -1/2 and the reciprocal of that is -2.
so now using either formula above you get:
y - 0 = -2(x -- 11) <--- Again remember -- is the same as +
y = -2x-2(11)
y = -2x - 22
or
y = mx +b
0 = -2(-11) + b
0 = 22 + b
-22 = b
y = -2x - 22
|
|
|
| |
