SOLUTION: The perimeter of a rectangle is 40, and the length of one of its diagonals is 10 \sqrt{2}. Find the area of the rectangle.

Let  'a'  and  'b'  be the lengths of two adjacent sides of the rectangle.


Then 

    a + b = 40/2 = 20,

    a^2 + b^2 = 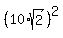 = 200.


Thus we have  b = 20-a,  and we substitute it into the second equation

    a^2 + (20-a)^2 = 200,

    a^2 + 400 - 40a + a^2 = 200,

    2a^2 - 40a + 200 = 0,

    a^2 - 20a + 100 = 0,

    (a-10)^2 = 0,

     a = 10.


Hence, the rectangle is a square with the side length of 10 units.


Thus the area of this rectangle (square) is  10^2 = 100 square untis.