.
Two matrices P and Q are
┌x² 3┐ and ┌3 6┐respectively.
│1 3x│ │2 x│
Given that P and Q are commutative under matrix multiplication. Find the positive value of x.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Two matrices are given
P = 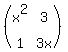 and Q =
and Q = 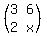 .
They are commutative under matrix multiplication. It means P*Q = Q*P.
We have
P*Q =
.
They are commutative under matrix multiplication. It means P*Q = Q*P.
We have
P*Q = 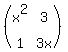 *
* 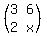 =
= 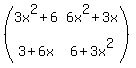 ,
Q*P =
,
Q*P = 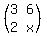 * (
* (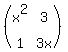 =
= 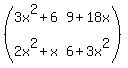 .
The expressions in cells (1,1) and (2,2) are identical, so, they are not interested for us.
From cells (1,2), we have this equation
6x^2 + 3x = 9 + 18x.
Cancel common factor 3
2x^2 + x = 3 + 6x (*)
2x^2 - 5x - 3 = 0,
(2x+1)*(x-3) = 0.
The roots are -1/2 and 3.
From cells (2,1), we have this equation
3+6x = = 2x^2+x.
It is identical to equation (*), so, it does not carry any new information.
Now we select positive root x = 3. It is the final answer:
+---------------------------------------------------+
| The problem has a unique answer x = 3 |
| for positive 'x'. |
| The matrices P and Q are commutative at x= 3. |
+---------------------------------------------------+
.
The expressions in cells (1,1) and (2,2) are identical, so, they are not interested for us.
From cells (1,2), we have this equation
6x^2 + 3x = 9 + 18x.
Cancel common factor 3
2x^2 + x = 3 + 6x (*)
2x^2 - 5x - 3 = 0,
(2x+1)*(x-3) = 0.
The roots are -1/2 and 3.
From cells (2,1), we have this equation
3+6x = = 2x^2+x.
It is identical to equation (*), so, it does not carry any new information.
Now we select positive root x = 3. It is the final answer:
+---------------------------------------------------+
| The problem has a unique answer x = 3 |
| for positive 'x'. |
| The matrices P and Q are commutative at x= 3. |
+---------------------------------------------------+
Solved.