Question 1210428: The third, fifth and tenth terms of a linear sequence (A.P.) form the first three terms of an exponential sequence (G.P.). If the sum of the second and fourth terms of the linear sequence (A.P.) is 18, find the:
(a) common difference of the linear sequence (A.P.);
(b) first term of the linear sequence (A.P.);
(c) sum of the first fifteen terms of the linear sequence (A.P.).
Answer by ikleyn(53354)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The third, fifth and tenth terms of a linear sequence (A.P.) form the first three terms
of an exponential sequence (G.P.). If the sum of the second and fourth terms of the linear sequence (A.P.) is 18,
find the:
(a) common difference of the linear sequence (A.P.);
(b) first term of the linear sequence (A.P.);
(c) sum of the first fifteen terms of the linear sequence (A.P.).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The sum of the second and fourth terms of the AP is its third term doubled.
It gives us that  = 18/2 = 9: the third term of the AP is 9.
Hence, the fifth and the tenth terms of this AP are = 18/2 = 9: the third term of the AP is 9.
Hence, the fifth and the tenth terms of this AP are  = 9 + 2d and = 9 + 2d and  = 9 + 7d.
Now we can write the proportion = 9 + 7d.
Now we can write the proportion
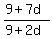 = = 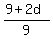 ,
saying that in the GP the ratio of the third term to the second term is equal to the ratio
of the second term to the first one (and equal to the common ratio of this GP).
From the proportion
(9+2d)*(9+2d) = 9*(9+7d),
81 + 18d + 18d + 4d^2 = 81 + 63d,
4d^2 - 27d = 0.
It gives two possible solutions for d: one solution d = 0, and another solution d = ,
saying that in the GP the ratio of the third term to the second term is equal to the ratio
of the second term to the first one (and equal to the common ratio of this GP).
From the proportion
(9+2d)*(9+2d) = 9*(9+7d),
81 + 18d + 18d + 4d^2 = 81 + 63d,
4d^2 - 27d = 0.
It gives two possible solutions for d: one solution d = 0, and another solution d = 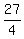 = 6.75.
It gives two possible answers for (a).
If d = 0, then the AP is 9, 9, 9, 9, . . .
so (b) the first term of the AP is 9,
and (c) the sum of the first 15 terms is 9*15 = 135.
If d = 6.75, then
(b) the first term of the AP is 9 - 2*6.75 = -4.5,
and (c) the sum of the first 15 terms is 641.25.
The last calculation for (c) is boring exercise, so I did it using online calculator
https://planetcalc.com/177/ = 6.75.
It gives two possible answers for (a).
If d = 0, then the AP is 9, 9, 9, 9, . . .
so (b) the first term of the AP is 9,
and (c) the sum of the first 15 terms is 9*15 = 135.
If d = 6.75, then
(b) the first term of the AP is 9 - 2*6.75 = -4.5,
and (c) the sum of the first 15 terms is 641.25.
The last calculation for (c) is boring exercise, so I did it using online calculator
https://planetcalc.com/177/
At this point, the problem is solved completely.
|
|
|