Question 1210402: There are 30 legs in my backyard but I'm counting dogs and kids.How many kids and dogs are in my backyard?
Found 4 solutions by josgarithmetic, ikleyn, MathTherapy, greenestamps:
Answer by josgarithmetic(39620)   (Show Source):
Answer by ikleyn(52814)  (Show Source):
You can put this solution on YOUR website! .
There are 30 legs in my backyard but I'm counting dogs and kids.
How many kids and dogs are in my backyard?
~~~~~~~~~~~~~~~~~~~~~~~~~~~
x dogs and y kids.
Counting the legs, we can write an equation
4x + 2y = 30.
Thus we have one equation in non-negative integer numbers in two unknowns.
+------------------------------------+
| It has more than one solution. |
+------------------------------------+
The possible solutions are listed in the Table below (every dog contributes 4 legs,
every kid contributes 2 legs)
x dogs y kids total legs
7 1 7*4 + 1*2 = 30
6 3 6*4 + 3*2 = 30
5 5 5*4 + 5*2 = 30
4 7 4*4 + 7*2 = 30
3 9 3*4 + 9*2 = 30
2 11 2*4 + 11*2 = 30
1 13 1*4 + 13*2 = 30
Solved.
----------------------------
How this problem is posed in your post, it reminds me a horse with 3 legs,
because it is posed in an absurdist way.
To be posed correctly, in addition to the number of legs, the problem should provide the total number of "heads",
i.e. the total number of the observed living beings in your backyards, which is missed in your post.
For similar problems, posed in a right way and solved properly, see the lessons
- Problem on animals at a farm
- Problem on pills in containers
- What type of problems are these?
in this site.
From reading these lessons, learn how to pose and how to write your problems correctly.
//////////////////////////////////////
Problems like these are classics of the genre. They've been around for hundreds of years, and many generations have learned from them.
Therefore, they should be treated with the utmost respect. This means writing them with extreme care - not like you're doing in your post.
Answer by MathTherapy(10555)  (Show Source):
You can put this solution on YOUR website!
There are 30 legs in my backyard but I'm counting dogs and kids.How many kids and dogs are in my backyard?
Let number of dogs, and kids, be D and K, respectively
As dogs have 4 legs, kids 2, and with a total 30 legs in the backyard, the following equation is derived:
4D + 2K = 30
2(2D + K) = 2(15)
2D + K = 15
2D = 15 - K
Number of dogs, or D =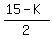 
As such, 15 - K is a non-NEGATIVE-INTEGER-MULTIPLE of 2, and so, K can ONLY be ODD, natural numbers from
1 to 13 (1,3,5,7,9,11, and 13). Therefore, unless some other info or clue is provided, there could be 7
DIFFERENT combinations of dogs and kids in the backyard.
A clue, such as, a COMPOSITE number of kids were present, would result in the number of kids being 9 (9 being the
ONLY composite number in the list of possibilities). It follows then, that there’d be 3 dogs, which makes sense,
since it’s more logical and “normal” to have 9 kids around 3 dogs (9:3, or 3:1 kids-to-dog ratio), as opposed to
1 kid around 7 dags (1:7 kid-to-dogs ratio), or 3 kids around 6 dogs (3:6, or 1:2 kid-to-dogs ratio).
Just SAYING!!
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
It should be clear from the given statement of the problem that there are many possible answers for the number of dogs.
Each dog has 4 legs; each kid has 2. Those are both even numbers, so the total number of legs for any numbers of dogs and kids will be even.
2 is the smallest even number, so you could have a total of 30 legs with only kids.
30 is not a multiple of 4, so you can't get a total of 30 legs with only dogs.
Obviously the number of dogs and the number of kids must be non-negative integers.
So the number of dogs can be any non-negative integer for which the total number of dog legs is less than 30.
ANSWER: The number of dogs can be any integer from 0 to 7 inclusive.
|
|
|
