Question 1210394: What is the inverse of Y=(X+3)² ?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630)   (Show Source):
Answer by ikleyn(52903)  (Show Source):
You can put this solution on YOUR website! .
What is the inverse of Y=(X+3)² ?
~~~~~~~~~~~~~~~~~~~~~~~~
The direct function (which is the given function) does the following:
- it adds the number 3 to the argument and then squares the value.
Therefore, the range of the given function is the set of all non-negative real numbers.
It means that the domain of the inverse function is the set of all non-negative real numbers,
and at this set the inverse function makes the opposite operations in reverse order:
- first, it takes square root from the value, and after that subtract 3 from the square root.
So, we can write an expression for the inverse function
g(x) =  - 3.
But square root from a real number can be positive or negative.
Therefore, there are TWO possible expressions for "the" inverse function.
First expression is p(x) = - 3, using positive value of .
Second expression is q(x) = - - 3, using negative value of .
These two possible expressions define two possible inverse functions.
Both inverse functions are defined over the set of non-negative real numbers.
First inverse function has the range [ , ).
Second inverse function has the range (-,].
At this point, the problem is solved completely, with detailed explanations, so everybody can understand.
----------------------------
It is important to note that the question in the problem is not precisely correct/accurate.
Indeed, it asks " what is the inverse function of Y =  ?"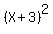
To be correct, in this situaion, the question should ask " what are possible inverse functions of Y = ?"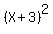
Now, after reading my post, you are armed to the teeth:
you know the right question and also know the right answer.
Come again to this forum soon to learn something new from the best source.
|
|
|
