Question 1210367: find the range of :
١) f(x) = sqrt(4 - x ^2) + x
٢)f(x)= sqrt(x- 3)- sqrt(x- 2)
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the range of f(x) = 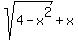
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Here in this my post, I will consider the problem (1), ONLY.
The solution to this problem can be done using Calculus, as tutor @greenestamps did it in his post.
But here I will show you how to solve it using elementary Algebra (the discriminant method).
Given function has the domain |x| <= 2, or -2 <= x <= 2.
The plot of the function is shown in the Figure below.
 Figure. Plot y =
Figure. Plot y =  + x (red line).
Blue line is the tangent line. Green line is a secant line.
As x grows starting from x = -2, the term + x (red line).
Blue line is the tangent line. Green line is a secant line.
As x grows starting from x = -2, the term  also grows.
So, in vicinity of x= -2, function also grows.
So, in vicinity of x= -2, function  is the sum of two monotonic terms;
therefore, it is also monotonically risen function there.
Then it gets its maximum value between 2 and 3 in 'y' somewhere between 1 and 2 in 'x'
and starts declining. It gets the value of 2 at x= 0 and x= 2.
Our task is to find the maximum of the function. As soon as we get it, we will solve the problem.
Seeking an elementary Algebra solution, let's introduce new variable is the sum of two monotonic terms;
therefore, it is also monotonically risen function there.
Then it gets its maximum value between 2 and 3 in 'y' somewhere between 1 and 2 in 'x'
and starts declining. It gets the value of 2 at x= 0 and x= 2.
Our task is to find the maximum of the function. As soon as we get it, we will solve the problem.
Seeking an elementary Algebra solution, let's introduce new variable
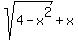 = t. (1)
Then = t. (1)
Then
 = t-x,
4 - x^2 = (t-x)^2 <<<---=== after squaring both sides in previous equation
4 - x^2 = t^2 - 2tx + x^2,
2x^2 - 2tx + (t^2-4) = 0. (2)
Out goal is to find the maximum value of 't'.
+----------------------------------------------------------------------------------------------+
| Equation (1) and the plot in the Figure tell us that maximum value of 't' is achieved |
| when two different possible roots 'x' of equation (1) merge into one single root. |
| |
| In terms of equation (2), it means that we want to consider equation (2) as an equation |
| for 'x' with parameter 't' and want to find 't' from the condition of merging its x-roots. |
+----------------------------------------------------------------------------------------------+
It means that we want to equate the discriminant of equation (2) to zero,
considering (2) as a quadratic equation for 'x'
0 = d = b^2 - 4ac = (-2t)^2 - 4*2*(t^2-4) = 4t^2 - 8t^2 + 32 = -4t^2 + 32,
or
4t^2 = 32 --> t^2 = 32/4 = 8 --> t = +/- = t-x,
4 - x^2 = (t-x)^2 <<<---=== after squaring both sides in previous equation
4 - x^2 = t^2 - 2tx + x^2,
2x^2 - 2tx + (t^2-4) = 0. (2)
Out goal is to find the maximum value of 't'.
+----------------------------------------------------------------------------------------------+
| Equation (1) and the plot in the Figure tell us that maximum value of 't' is achieved |
| when two different possible roots 'x' of equation (1) merge into one single root. |
| |
| In terms of equation (2), it means that we want to consider equation (2) as an equation |
| for 'x' with parameter 't' and want to find 't' from the condition of merging its x-roots. |
+----------------------------------------------------------------------------------------------+
It means that we want to equate the discriminant of equation (2) to zero,
considering (2) as a quadratic equation for 'x'
0 = d = b^2 - 4ac = (-2t)^2 - 4*2*(t^2-4) = 4t^2 - 8t^2 + 32 = -4t^2 + 32,
or
4t^2 = 32 --> t^2 = 32/4 = 8 --> t = +/-  .
The negative value for t is, obviously, irrelevant/extraneous, and we reject it.
The positive value t = .
The negative value for t is, obviously, irrelevant/extraneous, and we reject it.
The positive value t =  gives the maximum value of the given function.
So, the range of the given function is [ gives the maximum value of the given function.
So, the range of the given function is [  , , ], giving the ANSWER to the problem's question. ], giving the ANSWER to the problem's question.
At this point, the problem is solved completely.
In my solution, the explanation in the framed rectangle is very important.
It explains why we should interpret equation (2) as an equation relative variable x
and what form of the discriminant to use.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) 
The function has a real value only when the radicand is non-negative, so the domain of the function is [-2,2].
For the minimum value of the function, note that  is monotonically increasing, so the minimum value of f(x) will be when is monotonically increasing, so the minimum value of f(x) will be when  has its minimum value of zero. h(x)=0 when x=-2 and when x=2; that means f(x) has its minimum value when x=-2. So the minimum value of f(x) is has its minimum value of zero. h(x)=0 when x=-2 and when x=2; that means f(x) has its minimum value when x=-2. So the minimum value of f(x) is  . .
For the maximum value of f(x), we can use calculus. (There might be a relatively easy algebraic way to find the maximum value of f(x), but I'm not seeing it.)
The maximum value of f(x) is when the derivative is zero.








f(x) has its maximum value when x = sqrt(2).

The maximum value of f(x) is 2*sqrt(2).
ANSWER: The range of f(x) is [-2,2sqrt(2)]
(2) 
The function has a real value only when both radicands are non-negative, so the domain of the function is [3,infinity]
Note for all values in the domain, 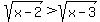 , so f(x) is always negative. , so f(x) is always negative.
As x increases towards infinity, the difference between  and and 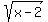 becomes infinitesimally small, so the function value gets arbitrarily close to 0 but never reaches it. becomes infinitesimally small, so the function value gets arbitrarily close to 0 but never reaches it.
And common sense says that the minimum value of f(x) is when x is minimum, which is when x=3. At that value of x,  . So the minimum value of f(x) is -1. . So the minimum value of f(x) is -1.
ANSWER: the range of f(x) is [-1,0)
|
|
|