Question 1210364: Let z1 and z2 be two complex numbers such that |z1| = 5 and z1/z2 + z2/z1 = 0. Find |z1 - z2|^2.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve the problem:
Let $z_1$ and $z_2$ be two complex numbers.
We are given two conditions:
1. $|z_1| = 5$
2. $\frac{z_1}{z_2} + \frac{z_2}{z_1} = 0$
From the second condition, we can multiply by $z_1 z_2$ (assuming $z_1 \neq 0$ and $z_2 \neq 0$, which must be true since $|z_1| = 5$ and if $z_2=0$ the expression is undefined):
$z_1^2 + z_2^2 = 0$
$z_1^2 = -z_2^2$
Now, let's take the modulus of both sides:
$|z_1^2| = |-z_2^2|$
$|z_1|^2 = |-1| |z_2|^2$
$|z_1|^2 = 1 \cdot |z_2|^2$
$|z_1|^2 = |z_2|^2$
Since $|z_1| = 5$, we have:
$5^2 = |z_2|^2$
$25 = |z_2|^2$
So, $|z_2| = 5$.
Now we need to find $|z_1 - z_2|^2$.
We know that for any complex number $z$, $|z|^2 = z \bar{z}$.
So, $|z_1 - z_2|^2 = (z_1 - z_2)(\overline{z_1 - z_2})$
$|z_1 - z_2|^2 = (z_1 - z_2)(\bar{z_1} - \bar{z_2})$
$|z_1 - z_2|^2 = z_1 \bar{z_1} - z_1 \bar{z_2} - z_2 \bar{z_1} + z_2 \bar{z_2}$
$|z_1 - z_2|^2 = |z_1|^2 + |z_2|^2 - (z_1 \bar{z_2} + z_2 \bar{z_1})$
We already know $|z_1|^2 = 25$ and $|z_2|^2 = 25$. So:
$|z_1 - z_2|^2 = 25 + 25 - (z_1 \bar{z_2} + z_2 \bar{z_1})$
$|z_1 - z_2|^2 = 50 - (z_1 \bar{z_2} + z_2 \bar{z_1})$
Let's go back to the relation $z_1^2 = -z_2^2$.
We can write $z_1 = i z_2$ or $z_1 = -i z_2$.
Case 1: $z_1 = i z_2$
Then $\bar{z_1} = -i \bar{z_2}$.
Substitute these into $z_1 \bar{z_2} + z_2 \bar{z_1}$:
$z_1 \bar{z_2} + z_2 \bar{z_1} = (i z_2) \bar{z_2} + z_2 (-i \bar{z_2})$
$= i |z_2|^2 - i |z_2|^2$
$= 0$
Case 2: $z_1 = -i z_2$
Then $\bar{z_1} = i \bar{z_2}$.
Substitute these into $z_1 \bar{z_2} + z_2 \bar{z_1}$:
$z_1 \bar{z_2} + z_2 \bar{z_1} = (-i z_2) \bar{z_2} + z_2 (i \bar{z_2})$
$= -i |z_2|^2 + i |z_2|^2$
$= 0$
In both cases, $z_1 \bar{z_2} + z_2 \bar{z_1} = 0$.
Therefore,
$|z_1 - z_2|^2 = 50 - 0$
$|z_1 - z_2|^2 = 50$
The final answer is $\boxed{50}$.
Answer by ikleyn(52804)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let z1 and z2 be two complex numbers such that |z1| = 5 and z1/z2 + z2/z1 = 0. Find |z1 - z2|^2.
~~~~~~~~~~~~~~~~~~~~~~~
I will give here simple, short, clear and transparent solution.
Let complex number z be z = z1//z2.
Then z2/z1 is 1/z, and the given equation z1/z2 + z2/z1 = 0 means
z +  = 0,
z = = 0,
z = 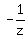 z^2 = -1
z =
z^2 = -1
z = 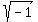 ,
z = i or z = -i.
If z = i, then z2 = i*z1, and
|z1 - z2|^2 = |z1 - i*z1)^2 = |z1|^2*|1-i|^2 = 5^2*((1-i)*(1+i)) = 25*(1-i^2) = 25*(1-(-1)) = 25*(1+1) = 25*2 = 50.
If z = -i, then z2 = -i*z1, and
|z1 - z2|^2 = |z1 + i*z1)^2 = |z1|^2*|1+i|^2 = 5^2*((1+i)*(1-i)) = 25*(1-i^2) = 25*(1-(-1)) = 25*(1+1) = 25*2 = 50.
ANSWER. Under given conditions, |z1-z2|^2 = 50. ,
z = i or z = -i.
If z = i, then z2 = i*z1, and
|z1 - z2|^2 = |z1 - i*z1)^2 = |z1|^2*|1-i|^2 = 5^2*((1-i)*(1+i)) = 25*(1-i^2) = 25*(1-(-1)) = 25*(1+1) = 25*2 = 50.
If z = -i, then z2 = -i*z1, and
|z1 - z2|^2 = |z1 + i*z1)^2 = |z1|^2*|1+i|^2 = 5^2*((1+i)*(1-i)) = 25*(1-i^2) = 25*(1-(-1)) = 25*(1+1) = 25*2 = 50.
ANSWER. Under given conditions, |z1-z2|^2 = 50.
Solved.
|
|
|