|
Question 1210281: a 50m supporting wire is to be attached to a 75 m antenna. Because of surrounding buildings, sidewalks, and roadways, the wire must be anchored exactly 20 m from the base of the antenna. How high from the top of the antenna is the wire attached?
Answer by ikleyn(52792)   (Show Source):
You can put this solution on YOUR website! .
a 50m supporting wire is to be attached to a 75 m antenna. Because of surrounding buildings,
sidewalks, and roadways, the wire must be anchored exactly 20 m from the base of the antenna.
How high from the top of the antenna is the wire attached?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let 'x' be the height of attaching the wire, from the ground.
We have a right-angled triangle "the ground - the antenna - the wire".
From this right-angled triangle,
x^2 + 20^2 = 50^2,
x^2 = 50^2 - 20^2 = 2500 - 400 = 2100
x = 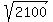 = 45.83 meters (rounded).
So, the distance of attaching from the top of the antenna is
75 - 45.83 = 29.17 meters. ANSWER
Solved.
Thanks for posting this problem.
I appreciate the accuracy of your post and clear language of your message.
|
|
|
| |
