SOLUTION: Find : limt((floor(x/3)-1)/(x-3)) , when (x→3)

The floor function rounds a real number x down to the nearest integer 
less than or equal to it. In other words, it returns the largest integer that is not greater than x.



        Notice that the given function is NOT defined at  x = 3.

        Due to this reason, the limit of the given function
        can not be determined directly.

        Let's consider this issue from different points of view.



When x approaches to 3 from the right side, 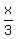   approaches to 1 from the right side.

Therefore, 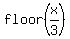 has then the value of 1 identically in vicinity of x= 3  on its right side.
 
Hence, function 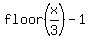   in the numerator is then identically 0 (zero) in vicinity of  x = 3  on its right side.

Therefore, the right limit of 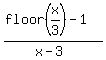   as x ---> 3  from the right side can be naturally defined as  0 (zero).



On the contrary, when x approaches to 3 from the left side, 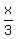   approaches to 1 from the left side.

Hence, function    is then identically -1  in vicinity of  x= 3  on its left side.

Therefore, the left limit of 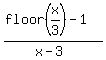  as x ---> 3  does not exist (is positive infinity).



Thus, as x ---> 3, the limit of the function 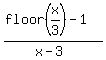   in the common sense does not exist.



ANSWER.  The given function is not defined at x = 3.

         The right limit of the given function at  x --> 3  is  (or can be defined as)  0 (zero);  

         the left limit of the given function at  x --> 3  does not exist;

         the limit of the given function at  x --> 3  in common sense does not exist and can not be defined.