Question 1210261: Acute triangle ABC has \sin A = \dfrac{2}{5} and \sin B = \dfrac{2}{\sqrt{7}}. What is \sin C?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Acute triangle ABC has sin(A) =  and sin(B) = and sin(B) = 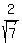 . What is sin(C) ? . What is sin(C) ?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Since sin(A) =  and angle A is acute (given), we have
A = and angle A is acute (given), we have
A = 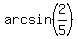 = 23.5781785 degrees.
Since sin(B) = = 23.5781785 degrees.
Since sin(B) = 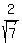 and angle B is acute (given), we have
B = and angle B is acute (given), we have
B = 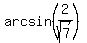 = arcsin(0.755928946) = 49.1066053 degrees.
Therefore, C = 180 - 23.5781785 - 49.1066053 = 107.3152162 degrees.
Then sin(C) = 0.95468179116.
ANSWER. sin(C) is about 0.95468179116. = arcsin(0.755928946) = 49.1066053 degrees.
Therefore, C = 180 - 23.5781785 - 49.1066053 = 107.3152162 degrees.
Then sin(C) = 0.95468179116.
ANSWER. sin(C) is about 0.95468179116.
Solved.
----------------------------------
A post-solution note
As I solved the problem to the end, I see that its formulation
is FATALLY INCORRECT and is SELF-CONTRADICTORY.
Indeed, the problem says that the given triangle is acute,
which means that all three its angles are acute.
But the angle C, as I found it, is OBTUSE: its measure is about 107 degrees.
So, this problem simply DECEIVES a reader,
which is  for a Math problem. for a Math problem.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
sin^2(A) + cos^2(A) = 1 ......... pythagorean trig identity
(2/5)^2 + cos^2(A) = 1
4/25 + cos^2(A) = 1
cos^2(A) = 1 - 4/25
cos^2(A) = 21/25
cos(A) = sqrt(21/25)
cos(A) = sqrt(21)/sqrt(25)
cos(A) = sqrt(21)/5
sin^2(B) + cos^2(B) = 1
(2/sqrt(7))^2 + cos^2(B) = 1
4/7 + cos^2(B) = 1
cos^2(B) = 1 - 4/7
cos^2(B) = 3/7
cos(B) = sqrt(3/7)
To summarize so far:
sin(A) = 2/5
cos(A) = sqrt(21)/5
sin(B) = 2/sqrt(7)
cos(B) = sqrt(3/7)
Then,
A+B+C = 180 degrees
C = 180-(A+B)
sin(C) = sin(180 - (A+B) )
sin(C) = sin(A+B) ........................................... use identity sin(180-x) = sin(x)
sin(C) = sin(A)cos(B) + cos(A)sin(B) ......................... angle sum identity
sin(C) = (2/5)*sqrt(3/7) + (sqrt(21)/5)*(2/sqrt(7))
sin(C) = 2*sqrt(3)/(5*sqrt(7)) + 2*sqrt(21)/(5*sqrt(7))
sin(C) = (2*sqrt(3) + 2*sqrt(21))/(5*sqrt(7))
sin(C) = 2*(sqrt(3) + sqrt(21))/(5*sqrt(7)) exactly
sin(C) = 0.9546817913107 approximately
----------------------------------------------------------------------------------------------------------------------
Another approach:
sin(A) = 2/5
A = arcsin(2/5)
A = 23.5781784782 degrees approximately
sin(B) = 2/sqrt(7)
B = arcsin(2/sqrt(7))
B = 49.10660535087 degrees approximately
A+B+C = 180
C = 180-A-B
C = 180-23.5781784782-49.10660535087
C = 107.31521617093
sin(C) = sin(107.31521617093)
sin(C) = 0.9546817913107 approximately
The drawback of this method is that you won't be able to determine the exact form in terms of square roots, as shown in the previous section.
However, some teachers are perfectly fine with the answer in decimal form.
|
|
|