Question 1210256: The volume of water increases by 8 1/2% when freezing. Determine amount of space water will occupy when frozen the volume is 1085 cu. ft.
Unsure how to solve.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Convert 8 1/2 % to 8.5%.
What you started with was 100%.
The INCREASE of 8.5% ADDS 8.5% to the original 100%, so the volume gets MULTIPLIED by 108.5% -- i.e., gets multiplied by 1.085.
If the original volume is 1085 cubic feet, then the new volume is (1085)*(1.085) = 1177.225 cubic feet.
ANSWER: the volume of the water AFTER freezing is 1177.225 cubic feet.
Note however, that the language/punctuation in your post is faulty, so it is possible that the given 1085 cubic feet is AFTER the water has frozen. If that is the case, then the given 1085 cubic feet must be DIVIDED by 1.085 to get the volume of the water before it was frozen. That of course gives a much nicer answer:
(1085)/(1.085) = 1000
ANSWER: the volume of the water BEFORE freezing was 1000 cubic feet.
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The volume of water increases by 8 1/2% when freezing.
Determine amount of space water will occupy when frozen the volume is 1085 cu. ft.
Unsure how to solve.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The problem says that if the volume of water is x, then the corresponding volume
of ice is 1.085x, and vice versa.
It is true for freezing process; for thawing/melting process, the liquid volume returns to its original value.
// These facts are well known. Normally, students learn them
// in middle school in their 6th or 7th grade, when they study Science.
Also, the problem gives the volume of ice 1085 cu. ft, and asks to find the corresponding volume of water.
It means that the problem itself is equivalent to this equation
1.085x = 1085 for the solid volume,
from which you should find the liquid volume x.
So, x = 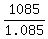 = 1000 cu ft. = 1000 cu ft.
At this point, the problem is solved in full.
To understand such problems in full and to solve them successfully,
the important first step is to make their formulation as straightforward as possible,
without losing their meaning.
|
|
|