Question 1210198: A standard deck of 52 cards has 13 ranks (Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King) and 4 suits (spades, hearts, diamonds, and clubs), such that there is exactly one card for any given rank and suit.
You are dealt a hand of 13 cards. Find the probability that your hand has a void. (Your hand has a void if it does not contain any cards of a particular suit.)
Once you've computed the answer in terms of binomial coefficients, use a calculator or computer to determine the answer to the nearest tenth of a percent, and enter that as your answer.
Found 3 solutions by CPhill, greenestamps, ikleyn:
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step by step.
**1. Total Number of Possible Hands**
* The total number of 13-card hands that can be dealt from a standard 52-card deck is:
* ⁵²C₁₃ = 52! / (13! * 39!) ≈ 6.35 × 10¹¹
**2. Number of Hands with a Void in a Specific Suit**
* Let's say we want to find the number of hands with a void in spades.
* If there are no spades, we are choosing 13 cards from the remaining 39 cards (52 - 13).
* ³⁹C₁₃ = 39! / (13! * 26!) ≈ 8.12 × 10¹⁰
**3. Number of Hands with a Void in Any Suit**
* Since there are 4 suits, we might think the total number of hands with a void is 4 * ³⁹C₁₃. However, we need to account for overlaps (hands with voids in multiple suits).
**4. Inclusion-Exclusion Principle**
We'll use the inclusion-exclusion principle to account for overlaps.
* Let A, B, C, D represent the events of having a void in spades, hearts, diamonds, and clubs, respectively.
* |A ∪ B ∪ C ∪ D| = |A| + |B| + |C| + |D| - |A ∩ B| - ... + |A ∩ B ∩ C| - |A ∩ B ∩ C ∩ D|
* **|A| = |B| = |C| = |D| = ³⁹C₁₃** (Number of hands with a void in one suit)
* **|A ∩ B| = |A ∩ C| = ... = ²⁶C₁₃** (Number of hands with voids in two suits)
* **|A ∩ B ∩ C| = |A ∩ B ∩ D| = ... = ¹³C₁₃** (Number of hands with voids in three suits)
* **|A ∩ B ∩ C ∩ D| = 0** (It's impossible to have voids in all four suits with a 13-card hand)
Therefore:
* |A ∪ B ∪ C ∪ D| = 4 * ³⁹C₁₃ - ⁶C₂ * ²⁶C₁₃ + ⁴C₃ * ¹³C₁₃
**5. Calculate the Values**
* ³⁹C₁₃ = 8122425444
* ²⁶C₁₃ = 10400600
* ¹³C₁₃ = 1
* |A ∪ B ∪ C ∪ D| = 4 * 8122425444 - 6 * 10400600 + 4 * 1
* |A ∪ B ∪ C ∪ D| = 32489701776 - 62403600 + 4
* |A ∪ B ∪ C ∪ D| = 32427298180
**6. Calculate the Probability**
* Probability = |A ∪ B ∪ C ∪ D| / ⁵²C₁₃
* Probability = 32427298180 / 635013559600 ≈ 0.051065
**7. Convert to Percentage and Round**
* 0.051065 * 100% ≈ 5.1065%
* Rounded to the nearest tenth of a percent: 5.1%
**Therefore, the probability that your hand has a void is approximately 5.1%.**
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The number of 13-card hands is "52 choose 13", which (rounded) is 6.35x10^11.
The number of 13-card hands that contains none of a particular one of the 4 suits is "39 choose 13", which is (rounded) 8.12x10^9.
The probability that a 13-card hand contains none of one suit is then
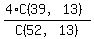
which is 0.05116379.... As a percentage rounded to a tenth of a percent, that is...
ANSWER: 5.1%
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution by @CPhill is unjustifiably complicated.
In plain English, it is not adequate, and therefore, I do not recommend it as a teaching tool.
See the solution in the post by @greenestamps.
That solution is what is expected in this problem.
From the point of view of AI (artificial intelligence), the solution
by @CPhill is not the item to save it and/or to keep it in the AI database.
In opposite, this @CPhill' solution should not be included
in the AI database under any circumstances.
|
|
|