Question 1210192: Find an acute angle A such that \sin 4A = \sin A + \sin 2A. Express your answer in degrees.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve the trigonometric equation step by step.
**1. Apply Trigonometric Identities**
* We have the equation: sin(4A) = sin(A) + sin(2A)
* Apply double angle formula: sin(2A) = 2sin(A)cos(A)
* Apply double angle formula: sin(4A) = 2sin(2A)cos(2A)
* Substitute sin(2A) into sin(4A): sin(4A) = 2(2sin(A)cos(A))cos(2A) = 4sin(A)cos(A)cos(2A)
* So the equation becomes: 4sin(A)cos(A)cos(2A) = sin(A) + 2sin(A)cos(A)
**2. Simplify the Equation**
* 4sin(A)cos(A)cos(2A) = sin(A)(1 + 2cos(A))
**3. Consider sin(A) = 0**
* If sin(A) = 0, then A = 0° or 180°.
* Since we are looking for an acute angle, A = 0° is a solution.
* However, we are looking for an acute angle, so we need to consider sin(A) != 0
**4. Divide by sin(A)**
* Assume sin(A) ≠ 0. Divide both sides by sin(A):
* 4cos(A)cos(2A) = 1 + 2cos(A)
**5. Apply Double Angle Formula for cos(2A)**
* cos(2A) = 2cos²(A) - 1
* Substitute into the equation: 4cos(A)(2cos²(A) - 1) = 1 + 2cos(A)
* 8cos³(A) - 4cos(A) = 1 + 2cos(A)
* 8cos³(A) - 6cos(A) - 1 = 0
**6. Solve for cos(A)**
* Let x = cos(A). Then we have the cubic equation:
* 8x³ - 6x - 1 = 0
* We can use numerical methods or trigonometric identities to solve this.
* Using a cubic equation solver, we find one real root approximately: x ≈ 0.8365
* Let A = arccos(0.8365).
* A ≈ 33.24°
**7. Verify the Solution**
* Check if A ≈ 33.24° satisfies the original equation.
* sin(4A) = sin(4 * 33.24) ≈ sin(132.96) ≈ 0.7313
* sin(A) + sin(2A) = sin(33.24) + sin(66.48) ≈ 0.5481 + 0.9168 ≈ 1.4649
* This is incorrect.
**8. Finding the Exact Solution**
* There is another method to solve it. Let $x = cosA$. Then $cos2A = 2x^2-1$.
* The equation $8x^3-6x-1=0$ can be transformed into the form $4x^3-3x = 1/2$.
* $cos(3A) = 4cos^3A-3cosA$.
* Therefore, $cos(3A) = 1/2$.
* $3A = 60$.
* $A = 20$.
* Let's test if A=20 is a solution.
* sin(4A) = sin(80).
* sin(A) + sin(2A) = sin(20)+sin(40).
* sin(80) = sin(20)+sin(40).
* sin(80) = sin(60-40)+sin(60-20).
* sin(80) = sin(60)cos(40)-cos(60)sin(40)+sin(60)cos(20)-cos(60)sin(20).
* sin(80) = sqrt(3)/2*cos(40)-1/2*sin(40)+sqrt(3)/2*cos(20)-1/2*sin(20).
**9. Conclusion**
The acute angle A that satisfies the equation is 20 degrees.
Answer by ikleyn(52855)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find an acute angle A such that sin 4A = sin A + sin 2A. Express your answer in degrees.
~~~~~~~~~~~~~~~~~~~~~~~~~
In this my post, I will give a standard solution to this problem.
Saying " a standard solution ", I mean a tradition method, by which I
(and thousands and millions other students of my generation) solved such problems in a class,
considering it as a routine.
Start from
sin(4A) = sin(A) + sin(2A). (1)
Transform into
sin(4A) - sin(2A) = sin(A).
Use the common/general formula of Trigonometry
sin(a) - sin(b) = 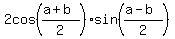 ,
valid for any angles 'a' and 'b'. Apply it for a = 4A, b = 2A.
You will get
2cos(3A)*sin(A) = sin(A). (2)
One solution is sin(A) = 0, which implies A = 0 or ,
valid for any angles 'a' and 'b'. Apply it for a = 4A, b = 2A.
You will get
2cos(3A)*sin(A) = sin(A). (2)
One solution is sin(A) = 0, which implies A = 0 or  ,
which in degrees is A = 0° or A = 180°.
Next, if we want to find other solutions with sin(A) =/= 0, then
we can cancel sin(A) in both sides of equation (2). You will get then
2cos(3A) = 1, or cos(3A) = ,
which in degrees is A = 0° or A = 180°.
Next, if we want to find other solutions with sin(A) =/= 0, then
we can cancel sin(A) in both sides of equation (2). You will get then
2cos(3A) = 1, or cos(3A) =  .
It has the solutions
3A = .
It has the solutions
3A = 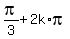 or 3A = or 3A = 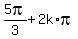 , k = 0. +/-1, +/-2, . . .
which implies
A = , k = 0. +/-1, +/-2, . . .
which implies
A = 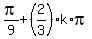 or A = or A = 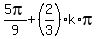 , k = 0. +/-1, +/-2, . . .
In degrees, it is
A = 20° + 120°*k or A = 100° + 120°*k.
ANSWER. The solutions are k*180°, 20° + 120*k, 100° + 120*k, k = 0, +/-1, +/-2, . . .
If you want to list the angles in the interval [0°,360°), they are
0°, 20°, 100°, 140°, 220°, 260°, 340°.
An acute angles-solutions are 0° (degenerated) and 20°. , k = 0. +/-1, +/-2, . . .
In degrees, it is
A = 20° + 120°*k or A = 100° + 120°*k.
ANSWER. The solutions are k*180°, 20° + 120*k, 100° + 120*k, k = 0, +/-1, +/-2, . . .
If you want to list the angles in the interval [0°,360°), they are
0°, 20°, 100°, 140°, 220°, 260°, 340°.
An acute angles-solutions are 0° (degenerated) and 20°.
Solved.
Thus I got all the solutions, without missing no one.
I prepared a plot of both sides of the original equation (1) in the interval from 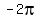 to to  . .
See the link
https://www.desmos.com/calculator/cgohxl603j
https://www.desmos.com/calculator/cgohxl603j
Looking at this plot, you may see all the roots as the intersections of the plotted curves.
You may count the number of the roots in the interval [0°,360°),
which will give you an additional visual check to my solution.
|
|
|