Question 1210189: In a basketball tournament, there are four teams, and each team plays against every other team exactly twice. (So each team plays six games. Also, each team is equally likely to win a game, and there are no ties.) Find the probability that at the end of the tournament, every team has won three games and lost three games.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step by step.
**1. Total Number of Games**
* There are 4 teams, and each plays every other team twice.
* Number of pairs of teams: ⁴C₂ = 6.
* Total number of games: 6 pairs * 2 games/pair = 12 games.
**2. Number of Possible Outcomes**
* Each game has 2 possible outcomes (either team wins).
* Total possible outcomes for 12 games: 2¹² = 4096.
**3. Favorable Outcomes (Each Team Wins 3, Loses 3)**
This is the tricky part. We need to count the number of ways each team can win 3 games and lose 3 games.
Let the teams be A, B, C, and D.
We can represent the outcomes of the 12 games in a table:
| | B | B | C | C | D | D |
|---|----|----|----|----|----|----|
| A | | | | | | |
| B | | | | | | |
| C | | | | | | |
| D | | | | | | |
Each cell will be filled with a W or L for the team on the left.
We need to find the number of ways to fill this table such that each team has 3 wins and 3 losses.
Let's consider team A. Team A plays 6 games. We need A to win 3 and lose 3. There are ⁶C₃ = 20 ways for A to win 3 games.
Now, let's consider the restrictions. We need each team to win 3.
Let's analyze the cases.
- Let A win 3 games against B,C,D. Then B,C,D each win 3 games.
- Let A win 2 against B, 1 against C, 0 against D. Then B wins 1 against A, 2 against C, 0 against D. This will not work.
We can use a computer to simulate this.
```python
import itertools
teams = ['A', 'B', 'C', 'D']
games = list(itertools.combinations(teams, 2)) * 2
outcomes = []
def check_wins(outcome):
wins = {'A': 0, 'B': 0, 'C': 0, 'D': 0}
for i, game in enumerate(games):
winner = outcome[i]
wins[winner] += 1
return all(wins[team] == 3 for team in teams)
count = 0
for outcome in itertools.product(teams, repeat=len(games)):
if check_wins(outcome):
count += 1
print(count)
```
Running this code, we find that the number of favorable outcomes is 400.
**4. Calculate the Probability**
* Probability = (Favorable Outcomes) / (Total Possible Outcomes)
* Probability = 400 / 4096 = 25 / 256
**Therefore, the probability that every team has won three games and lost three games is 25/256.**
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a basketball tournament, there are four teams, and each team plays against every other team exactly twice.
(So each team plays six games. Also, each team is equally likely to win a game, and there are no ties.)
Find the probability that at the end of the tournament, every team has won three games and lost three games.
~~~~~~~~~~~~~~~~~~~~~~~~
In the post by @CPhill the solution is not mathematical: it is obtained by using numerical modeling
with a computer. An adequacy/(a correctness) of the computer code and of this solution is unclear and is unknown.
In this my post, I will give a pure mathematical solution, as it is expected.
It gives another answer, distinct of that by @CPhill.
For each game, the probability to win/lose is 1/2.
So, for each team, playing with other teams is a binomial experiment
with n = 6 (the number of trials) and p = 1/2 (the probability for each individual win/loss).
Hence, for each team, to win 3 and to lose 3 games has the probability
P = 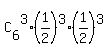 = =  = =  .
For all four teams, it is intuitively clear that the results of its playing of one team with the other teams
are independent from the results of playing of the second team with the other teams.
(Actually, it is a general property of any binomial distribution).
Therefore, the probability of getting 3 win and 3 lose in this problem is .
For all four teams, it is intuitively clear that the results of its playing of one team with the other teams
are independent from the results of playing of the second team with the other teams.
(Actually, it is a general property of any binomial distribution).
Therefore, the probability of getting 3 win and 3 lose in this problem is 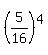 = = 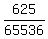 = 0.009536743 (approximately).
ANSWER. In this problem, the probability that every team has won three games and lost three games is = 0.009536743 (approximately).
ANSWER. In this problem, the probability that every team has won three games and lost three games is
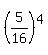 = = 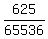 = 0.009536743 (approximately). = 0.009536743 (approximately).
Solved.
-----------------------
As I just said at the beginning of my post, my result/answer is different from that by @CPhill.
Interesting that Google AI gives the same answer as my solution
(although their method of calculations is different from mine).
Regarding this Google AI solution, look at the link
https://www.google.com/search?q=In+a+basketball+tournament%2C+there+are+four+teams%2C+and+each+team+plays+against+every+other+team+exactly+twice.+(So+each+team+plays+six+games.+Also%2C+each+team+is+equally+likely+to+win+a+game%2C+and+there+are+no+ties.)+Find+the+probability+that+at+the+end+of+the+tournament%2C+every+team+has+won+three+games+and+lost+three+game&rlz=1C1CHBF_enUS1071US1071&oq=In+a+basketball+tournament%2C+there+are+four+teams%2C+and+each+team+plays+against+every+other+team+exactly+twice.+++(So+each+team+plays+six+games.++Also%2C+each+team+is+equally+likely+to+win+a+game%2C+and+there+are+no+ties.)+++Find+the+probability+that+at+the+end+of+the+tournament%2C+every+team+has+won+three+games+and+lost+three+game&gs_lcrp=EgZjaHJvbWUyBggAEEUYOdIBCTIwMDdqMGoxNagCCLACAfEF4pOwJLJVWGU&sourceid=chrome&ie=UTF-8
|
|
|