Question 1210173: Let P be a point chosen uniformly at random inside triangle ABC. Extend ray BP to hit side AC at D. What is the probability that BD < 4?
The sides of triangle ABC are 3, 5, and 7.
Found 8 solutions by CPhill, Edwin McCravy, ikleyn, mccravyedwin, AnlytcPhil, greenestamps, McCravyE, EPM:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Let's break down this problem step by step.
**1. Geometric Interpretation**
We are looking for the probability that BD < 4. This is equivalent to finding the area of the region inside triangle ABC where BD < 4, and dividing it by the total area of triangle ABC.
**2. Triangle ABC and Ray BP**
* Let P be a random point inside triangle ABC.
* Ray BP intersects AC at point D.
* We want to find the probability that BD < 4.
**3. Law of Cosines**
Let's find the angles of triangle ABC using the Law of Cosines:
* Let a = 3, b = 5, c = 7.
* $\cos A = \frac{b^2 + c^2 - a^2}{2bc} = \frac{25 + 49 - 9}{2(5)(7)} = \frac{65}{70} = \frac{13}{14}$
* $\cos B = \frac{a^2 + c^2 - b^2}{2ac} = \frac{9 + 49 - 25}{2(3)(7)} = \frac{33}{42} = \frac{11}{14}$
* $\cos C = \frac{a^2 + b^2 - c^2}{2ab} = \frac{9 + 25 - 49}{2(3)(5)} = \frac{-15}{30} = -\frac{1}{2}$
Since $\cos C = -1/2$, angle C = 120 degrees.
**4. Area of Triangle ABC**
We can use Heron's formula to find the area of triangle ABC.
* Semi-perimeter: $s = (3 + 5 + 7)/2 = 15/2 = 7.5$
* Area = $\sqrt{s(s-a)(s-b)(s-c)} = \sqrt{7.5(4.5)(2.5)(0.5)} = \sqrt{42.1875} = \frac{15\sqrt{3}}{4}$
**5. Geometric Reasoning**
* Let's consider the locus of points P inside triangle ABC such that BD = 4.
* We can create a triangle ABD' where BD' = 4.
* The locus of P such that BD = 4 is a line parallel to AD'.
* The region where BD < 4 is the region inside triangle ABC that is closer to B than to D'.
**6. Ratio of Areas**
* The probability we are looking for is the ratio of the area of the region where BD < 4 to the area of the triangle ABC.
* Let's consider a point P that makes BD = 4.
* Let's determine the ratio of AD/CD.
* By the Angle Bisector Theorem, if P were to lie on an angle bisector, we could find the ratios. However, P is not necessarily on an angle bisector.
* The ratio AD/CD is dependent on the position of point P.
**7. Difficulties**
* Determining the exact shape of the region where BD < 4 is challenging without further geometric constructions and calculations.
* The problem requires a more advanced approach, potentially involving barycentric coordinates or other geometric methods.
**8. Conclusion**
Without further information or a more advanced approach, it's difficult to find the exact probability. However, we know that the probability is the ratio of the area of the region where BD < 4 to the total area of the triangle.
Unfortunately, I don't see a way to solve this problem without more advanced techniques.
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website!
The figure is drawn to scale.
BD' is exactly 4 units. So the point P must be chosen inside triangle
ABD' in order for BD to be < 4, as shown in the red part.
So we want the probability that point P is chosen inside triangle ABD'. which
will be:
I don't have time right now to find the areas of those two triangles. Maybe
another tutor will do that. Otherwise, I'll be back tomorrow.
Edwin
Answer by ikleyn(52797)  (Show Source):
You can put this solution on YOUR website! .
Let P be a point chosen uniformly at random inside triangle ABC. Extend ray BP to hit side AC at D.
What is the probability that BD < 4?
The sides of triangle ABC are 3, 5, and 7.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
After checking my previous solution one more time, I found an error in it.
After that, I fixed the error, and now I place this my updated solution here AGAIN.
Edwin was right in that my previous solution was incorrect.
Sorry for that and thanks to Edwin for helping me to detect my error.
Below you see this my corrected version.
S O L U T I O N
I will borrow the picture from the post by Edwin with my "thanks".
From the given side lengths, we
(a) will determine cos(A) using the cosine low;
(b) will determine a position of the point D' in the figure;
(c) then the probability is the ratio of the area of triangle BAD' to the area of triangle BAC,
and this ratio is nothing else as the ratio of the length AD' to AC. .
Below is the implementation of these steps.
(a) According to the cosine law,
7^2 = 3^2 + 5^2 - 2*3*5*cos(A).
It gives
cos(A) = 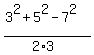 = -0.5.
(b) We want to find a point D' such that the length of BD' is 4.
Let BD' be x.
Use the cosine law again
4^2 = 3^2 + x^2 - 2*3*x*cos(A),
4^2 = 3^2 + x^2 - 2*3*x*(-1/2),
4^2 = 3^2 + x^2 + 3x
x^2 + 3x + 3^2 - 4^2 = 0,
x^2 + 3x - 7 = 0
 =  =  .
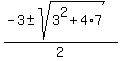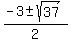Reject the negative root and accept the positive one x = 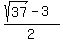 = 1.541381265.
(c) Thus the length of BD' is 1.541381265 unit.
So, the probability under the problem's question is the ratio of AD' to AC,
which is 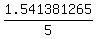 = 0.308276253.
Notice that numerically it is the same answer as in the post by Edwin.
ANSWER. The probability under the problem's question is 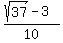 , or 0.308276253, approximately.
Solved.
/////////////////////////////
Addition.
This addition is for Edwin and for those who tracked the events around this problem.
Edwin criticized me for the statement
(c) then the probability is the ratio of the area of triangle BAD' to the area of triangle BAC,
and this ratio is nothing else as the ratio of the length AD' to AC.
This my statement is   , and it   as a  .
The error was in deriving the quadratic equation.
Originally, I derived it with the error, but when I fixed this error, I got everything correct.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Edwin asks me
How do you know this:
The ratio of the area of triangle BAD' to the area of triangle BAC
equals the ratio of the length AD' to AC.
What theorem shows this is true?
Edwin, I will prove it right now. The proof is a simple Geometry exercise.
Prolong the line CA from 'C' to 'A' and further to the left and up.
Draw a perpendicular from vertex B to this prolonged line CA to the intersection at some point E.
Then BE is the common height/altitude for triangles BAD' and BAC;
the bases for these triangles are AD' and AC, respectively.
Let 'h' denotes the length of BE: h = |BE|.
Write formulas for areas of triangles BAD' and BAC
area[BAD'] = 0.5*h*|AD'|, area [BAC] = 0.5*h*|AC|.
From these formulas, you should see that ratio of the area of triangle BAD' to the area of triangle BAC
equals the ratio of the length AD' to the length of AC.
The proof is complete.
Again, the proof is at the introductory Geometry level.
I think that it is should be SELF-EVIDENT to any ordinary average level student.
If you want I formulate it as a Theorem, here it is:
If two triangles have common altitude, then the ratio of the areas of these triangles
equals to the ratio of the bases of these triangles.
You may attribute this theorem to me and call it "The Kleyn's theorem".
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
All Edwin' exclamations in his posts, related to this problem and stating
that my arguments are incorrect, are erroneous.
So, for safety of your mind, ignore all of them.
The fact that Edwin still has not cancel these exclamations
on his own after all our discussions is simply his oversight.
Answer by mccravyedwin(407)  (Show Source):
You can put this solution on YOUR website!
Ikleyn has made a false assumption, when she said:
"...the ratio of the area of triangle BAD' to the area of triangle BAC,
...is nothing else [but] the ratio of the length AD' to AC.
While it is true that a PERPENDICULAR drawn from a vertex to the opposite
side of a triangle divides the opposite side into the same ratio as the ratio
of the areas of the right triangles formed by the perpendicular, this is NOT
true when the line is not perpendicular to the opposite side.
Ikleyn was apparently thinking of what would have been the case if BD' had been
perpendicular to AC, which it is not.
She was thinking of this case:
We see from this, that the ratio she assumed would be correct.
But that only holds when the line from the vertex to the opposite side is
perpendicular to the opposite side. But in the original figure BD' is not
perpendicular to AC.
The only way to do the problem is to find the actual areas and compare them.
Ikleyn has used the law of cosines to find the cosine to be that of a special
angle, 120o. So we could then use the sine of that special angle and the area
formula using the sine to find the area of triangle ABC.
Then we could use the law of cosines again on triangle ABD' to find side AD'.
Then we could use the area formula using the sine again to find the area of
triangle ABD'.
If Ikleyn wants to correct her post, I will then delete this one, and make
another post using a different screen name to inform the student that the correct
solution is now online, and which tutor gave it.
I'll give Ikleyn a couple of days to do this. If she hasn't done it by Monday,
I will delete this, and post the correct solution under a different screen name.
Edwin
Answer by AnlytcPhil(1806)  (Show Source):
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Also borrowing the diagram from Edwin, and modifying it some for my use....
If point D is anywhere on AE between A and E (i.e., if point P is inside triangle ABE), the length of BD will be less than 4, as required.
(1) Use Heron's formula to find the area of triangle ABC.
(2) Use Stewart's Theorem to determine the length of AE.
 (ignore the negative root!)
(3) use the law of cosines to find the measure of angle A.
The measure of angle A is 120 degrees.
(4) Find the area of triangle ABE using area = (1/2)(AB)(BE)sin(A).
Cos(A) is 0.5, and angle A is obtuse, so sin(A) is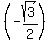 
(5) The probability in the question is the ratio of the areas of triangles ABE and ABC:
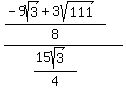
To several decimal places that number is 0.30828.
ANSWER: The probability is approximately 0.30828, or about 30.8%
That agrees with the answer Edwin got -- reached by a very different path.
And now a final note on this problem....
In Edwin's figure, vertex B is opposite the side with length 5, leading to the solution above.
However, there is nothing in the statement of the problem -- either specific or implied -- that that is the case.
And, indeed, it is easy to see that if B is the vertex opposite the side with length 3, the length of AD will NEVER be less than 4; and if B is opposite the side with length 7, the length of AD will ALWAYS be less than 4.
Since we could choose (with equal probability) any of the vertices of triangle ABC to be angle B, perhaps the ANSWER to the problem should be the average of the probabilities for the three cases:
Answer by McCravyE(1)  (Show Source):
You can put this solution on YOUR website!
My question to Ikleyn is:
How do you know this:
The ratio of the area of triangle BAD' to the area of triangle BAC, equals the ratio of the length AD' to AC.
What theorem shows this is true?
You didn't state any theorem that shows that. And it certainly is not obvious
to me.
Thanks for answering how you knew this to be true on your solution.
Edwin
Answer by EPM(3) (Show Source):
|
|
|
