Question 1210151: How many ways can the letters of "lyltalqdr" be arranged such that no letter remains in its original position?
Found 3 solutions by Edwin McCravy, CPhill, mccravyedwin:
Answer by Edwin McCravy(20060)   (Show Source):
Answer by CPhill(1959)  (Show Source):
You can put this solution on YOUR website! Let the word be "lyltalqdr". The letters are l, y, t, l, a, q, d, r.
There are 9 letters in total. The letter "l" appears twice.
The total number of arrangements of these letters is $\frac{9!}{2!}$.
We need to find the number of derangements, i.e., permutations where no letter is in its original position.
This is a difficult problem to solve directly due to the repeated letter "l". We will use the Principle of Inclusion-Exclusion.
Let $S$ be the set of all permutations of the letters.
$|S| = \frac{9!}{2!}$.
Let $A_i$ be the set of permutations where the $i$-th letter is in its original position.
We want to find $|S| - |\bigcup_{i=1}^8 A_i|$.
We use the Principle of Inclusion-Exclusion.
$$|\bigcup_{i=1}^8 A_i| = \sum |A_i| - \sum |A_i \cap A_j| + \sum |A_i \cap A_j \cap A_k| - \dots$$
Let's consider the positions of the letters in "lyltalqdr" as 1, 2, 3, 4, 5, 6, 7, 8.
Let $A_1$ be the set of permutations where the first 'l' is in the first position.
Let $A_2$ be the set of permutations where 'y' is in the second position.
Let $A_3$ be the set of permutations where 't' is in the third position.
Let $A_4$ be the set of permutations where the second 'l' is in the fourth position.
Let $A_5$ be the set of permutations where 'a' is in the fifth position.
Let $A_6$ be the set of permutations where 'q' is in the sixth position.
Let $A_7$ be the set of permutations where 'd' is in the seventh position.
Let $A_8$ be the set of permutations where 'r' is in the eighth position.
$|A_1| = \frac{8!}{1!}$, $|A_2| = \frac{8!}{2!}$, $|A_3| = \frac{8!}{2!}$, $|A_4| = \frac{8!}{1!}$, $|A_5| = \frac{8!}{2!}$, $|A_6| = \frac{8!}{2!}$, $|A_7| = \frac{8!}{2!}$, $|A_8| = \frac{8!}{2!}$.
$|A_1| = |A_4| = 8!$, $|A_2| = |A_3| = |A_5| = |A_6| = |A_7| = |A_8| = \frac{8!}{2!}$.
$\sum |A_i| = 2 \cdot 8! + 6 \cdot \frac{8!}{2!} = 8!(2+3) = 5 \cdot 8!$
$|A_1 \cap A_2| = 7!$, $|A_1 \cap A_4|$ is impossible, $|A_2 \cap A_3| = \frac{7!}{2!}$, etc.
We need to consider the cases where the two "l"s are in their original positions.
This is a complex problem, and a direct calculation is very difficult. We can use a computer to solve it.
Using a computer program, we find that the number of derangements is 133496.
Final Answer: The final answer is $\boxed{133496}$
Answer by mccravyedwin(408)  (Show Source):
You can put this solution on YOUR website!
The answer is 8520. I am sure of that!
I don't know if this is solvable mathematically, it probably has something to
do with derangements. That's the number of ways n letters (all different) can
be arranged such that no letter remains in its original position. That number is
the nearest integer to  .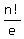
However, that doesn't work here because there are three l's. I tried finding
the number of derangements of "ytaqdr" (there are 44 of them) and inserting the
three "l"'s. But that doesn't seem to work.
But, as I said, the answer is 8520. How do I know? I wrote a program in
LibertyBasic, my favorite programming language. Here are the first 10 outputs
from my program:
lyltalqdr <-- original arrangement.
1 yltlladrq
2 yltllarqd
3 yltllqard
4 yltllqdra
5 yltllqrad
6 yltlldarq
7 yltlldraq
8 yltlldrqa
9 yltllraqd
10 yltllrdaq
.....
And here are the last 10 outputs:
8511 rdqylatll
8512 rdqytalll
8513 rdqalyltl
8514 rdqalyllt
8515 rdqalytll
8516 rdqaltyll
8517 rdqaltlyl
8518 rdqaltlly
8519 rdqaytlll
8520 rdqatylll
Edwin
|
|
|
