The ratio of adults to boys is 9 to 1.





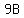 The ratio of adults to girls is 3 to 2.
The ratio of adults to girls is 3 to 2.



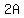

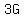 Since
Since 

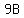 ,
, 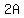

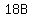 So
So
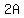

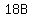

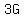
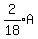

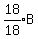

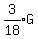
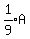

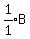

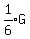
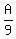

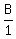

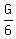
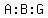

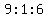 So at the start, there could have been 9 Adults, 1 Boy, and 6 Girls.
[Note: we cannot know the exact number there could have been at the start,
because there is not enough information given to find that. However, we can
assume any numbers at the start as long as we keep their ratios as we are
required to in the problem.]
When half of the adults....leave....
Oh, oh!, we need the number of adults at the start to be even, so that we can
take 1/2 without getting a fraction, so we double what there could have been at
the start:
So at the start, there could have been 18 Adults, 2 Boys, and 12 Girls.
Then after half the adults leave, there are only
So at the start, there could have been 9 Adults, 1 Boy, and 6 Girls.
[Note: we cannot know the exact number there could have been at the start,
because there is not enough information given to find that. However, we can
assume any numbers at the start as long as we keep their ratios as we are
required to in the problem.]
When half of the adults....leave....
Oh, oh!, we need the number of adults at the start to be even, so that we can
take 1/2 without getting a fraction, so we double what there could have been at
the start:
So at the start, there could have been 18 Adults, 2 Boys, and 12 Girls.
Then after half the adults leave, there are only 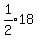

 adults remaining.
....and 2/3 of the girls leave,....
Then there are only
adults remaining.
....and 2/3 of the girls leave,....
Then there are only 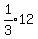

 girls remaining.
(It's OK to assume 12 girls at the start since we can take 1/3 of 12 without
getting a fraction).
What was the ratio of adults to boys to girls at the end?
adults:boys:girls = 9:2:4 <---ANSWER
Edwin
girls remaining.
(It's OK to assume 12 girls at the start since we can take 1/3 of 12 without
getting a fraction).
What was the ratio of adults to boys to girls at the end?
adults:boys:girls = 9:2:4 <---ANSWER
Edwin