Question 1209973: Let a and b be positive real numbers. Let
m = \min \left\{ a, \frac{1}{b}, b^2 + \frac{1}{a + 1} \right\}.
Find the largest possible value of m.
Found 4 solutions by CPhill, Edwin McCravy, ikleyn, mccravyedwin:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $m = \min \left\{ a, \frac{1}{b}, b^2 + \frac{1}{a+1} \right\}$.
We want to find the largest possible value of $m$.
Since $m$ is the minimum of the three quantities, we have
$$ m \le a, \quad m \le \frac{1}{b}, \quad m \le b^2 + \frac{1}{a+1}. $$
We want to maximize $m$, so we consider the case when all three quantities are equal to $m$:
$$ a = m, \quad \frac{1}{b} = m, \quad b^2 + \frac{1}{a+1} = m. $$
From $a=m$ and $\frac{1}{b} = m$, we get $a=m$ and $b=\frac{1}{m}$.
Substitute $a=m$ and $b=\frac{1}{m}$ into the third equation:
$$ \left( \frac{1}{m} \right)^2 + \frac{1}{m+1} = m. $$
$$ \frac{1}{m^2} + \frac{1}{m+1} = m. $$
Multiplying by $m^2(m+1)$, we get
$$ m+1 + m^2 = m^3(m+1). $$
$$ m+1 + m^2 = m^4 + m^3. $$
$$ m^4 + m^3 - m^2 - m - 1 = 0. $$
Let $f(m) = m^4 + m^3 - m^2 - m - 1$. We are looking for a positive real root.
We can test some values:
$f(1) = 1+1-1-1-1 = -1$
$f(2) = 16+8-4-2-1 = 17$
Since $f(1) < 0$ and $f(2) > 0$, there is a root between 1 and 2.
Let's consider the case when the three quantities are close to each other.
If we set $a = \frac{1}{b}$, then $ab = 1$.
Then we have $a = m$, $b = \frac{1}{m}$, and $b^2 + \frac{1}{a+1} = m$.
$$ \frac{1}{m^2} + \frac{1}{m+1} = m. $$
Let us try to find a simpler solution.
Suppose $a = \frac{1}{b} = b^2 + \frac{1}{a+1} = m$.
If $a = \frac{1}{b}$, then $ab=1$.
If $a = m$ and $\frac{1}{b} = m$, then $b=\frac{1}{m}$.
If $m = b^2 + \frac{1}{a+1}$, then $m = \frac{1}{m^2} + \frac{1}{m+1}$.
If we assume $m = 1$, then $a = 1$, $b = 1$, and $1 = 1^2 + \frac{1}{1+1} = 1 + \frac{1}{2} = \frac{3}{2}$, which is false.
Let's try to find a solution by setting $a = \frac{1}{b}$.
Then $m \le a$ and $m \le \frac{1}{b}$, so $m \le a$ and $m \le a$.
Also, $m \le b^2 + \frac{1}{a+1}$.
Since $b = \frac{1}{a}$, $m \le \frac{1}{a^2} + \frac{1}{a+1}$.
If $m = a$, then $a \le \frac{1}{a^2} + \frac{1}{a+1}$.
$a^3(a+1) \le a+1 + a^2$
$a^4 + a^3 \le a^2 + a + 1$
Let's consider the case when $a = \frac{1}{b} = b^2 + \frac{1}{a+1}$.
If $a=1$, then $b=1$.
$1 = 1^2 + \frac{1}{1+1} = 1 + \frac{1}{2} = \frac{3}{2}$, which is false.
If $m=1$, then $a=1$ and $b=1$.
Then $m = \min \left\{ 1, 1, 1^2 + \frac{1}{1+1} \right\} = \min \left\{ 1, 1, \frac{3}{2} \right\} = 1$.
Thus, $m=1$ is a possible value.
Let $a = 1.32$. $b = 1/a = 0.7575$. $b^2 + 1/(a+1) = 0.7575^2 + 1/2.32 = 0.5738 + 0.4310 = 1.0048$
If $m=1$, then $1 \le a$, $1 \le 1/b$, $1 \le b^2 + 1/(a+1)$.
$b \le 1$, $b^2 \ge 1-1/(a+1)$
$b^2 \ge a/(a+1)$.
$1/b \ge 1$, so $1/b \ge a$.
$1 \ge a/(a+1)b^2$, so $1/b^2 \ge a/(a+1)$.
$1/b^2 = a^2 \ge a/(a+1)$.
$a^2(a+1) \ge a$.
$a(a+1) \ge 1$.
$a^2+a-1 \ge 0$.
$a = (-1 \pm \sqrt{1+4})/2 = (-1 \pm \sqrt{5})/2$.
$a \ge (-1 + \sqrt{5})/2$.
If $m=1$, then $a \ge 1, b \le 1$, and $b^2 + \frac{1}{a+1} \ge 1$.
If $a=1$, $b=1$, $1 \le 1, 1 \le 1, 1 \le 3/2$.
Thus $m=1$ is possible.
Final Answer: The final answer is $\boxed{1}$
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I don't believe AI has the right answer.
Let a and b be positive real numbers. Let
 Find the largest possible value of m.
I can't prove it right off, but my better judgment tells me it's whatever
values of ' a ' and ' b ' that make all three expressions equal, IF there exist
any such values. I'll work on proving it, and if I succeed I'll post it. I hold
an MS degree in mathematics from Clemson University, but I never studied any
such topics as this in any course I ever took.
Find the largest possible value of m.
I can't prove it right off, but my better judgment tells me it's whatever
values of ' a ' and ' b ' that make all three expressions equal, IF there exist
any such values. I'll work on proving it, and if I succeed I'll post it. I hold
an MS degree in mathematics from Clemson University, but I never studied any
such topics as this in any course I ever took.
 WolframAlpha tells me such values do exist, and they are approximately
a=1.1787241761052217926, b=0.848374895731953217
They check with my TI-84 calculator.
So I believe the maximum is approximately 1.1787241761052217926
Edwin
WolframAlpha tells me such values do exist, and they are approximately
a=1.1787241761052217926, b=0.848374895731953217
They check with my TI-84 calculator.
So I believe the maximum is approximately 1.1787241761052217926
Edwin
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let a and b be positive real numbers.
Let m = min { a, 1/b, b^2 + 1/(a + 1).
Find the largest possible value of m.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We want to have
a =  , (1) , (1)
 + + 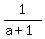 = =  (2)
Substitute expression (1) into equation (2). You will get (2)
Substitute expression (1) into equation (2). You will get
 + + 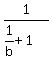 = =  .
Simplify this three-story fraction in the left side .
Simplify this three-story fraction in the left side
 + + 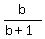 = =  .
Multiply both sides by b*(b+1). You will get
b^3*(b+1) + b^2 = b+1.
Write in the canonical polynomial form
b^4 + b^3 + b^2 - b - 1 = 0.
It can not be solved algebraically. Solve it numerically using specialized software
www.desmos.com/calculator.
The only positive root is b = 0.84837 (approximately).
See the plot, showing the root, under this link
https://www.desmos.com/calculator/tett0qlsmc <<<---=== it is the report on numerical solution
(Click on x-interception point to see the value of the root).
So, the solutions are b= 0.84837, a = .
Multiply both sides by b*(b+1). You will get
b^3*(b+1) + b^2 = b+1.
Write in the canonical polynomial form
b^4 + b^3 + b^2 - b - 1 = 0.
It can not be solved algebraically. Solve it numerically using specialized software
www.desmos.com/calculator.
The only positive root is b = 0.84837 (approximately).
See the plot, showing the root, under this link
https://www.desmos.com/calculator/tett0qlsmc <<<---=== it is the report on numerical solution
(Click on x-interception point to see the value of the root).
So, the solutions are b= 0.84837, a =  = =  = 1.17873 (close to the values in the post by Edwin).
The value of the expression = 1.17873 (close to the values in the post by Edwin).
The value of the expression  + + 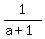 is is
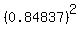 + +  = 1.17871.
Thus the approximate solution, derived this way, is
a = 1.17873, b = 0.84837, 1/b = 1/17873 = a, = 1.17871.
Thus the approximate solution, derived this way, is
a = 1.17873, b = 0.84837, 1/b = 1/17873 = a,  + + 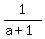 = 1.17871.
This set of values provides the maximum possible value of m = min ( a, = 1.17871.
This set of values provides the maximum possible value of m = min ( a,  , , 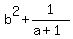 )
over all pairs of positive real numbers {(a,b)}. )
over all pairs of positive real numbers {(a,b)}.
Solved.
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I didn't bother to solve the system of equations, but let online technology
do that for me. Thanks to Ikleyn for solving them.
But the question that is still not answered is:
WHY does the maximum of the minimums occur when the three
expressions are equal?
It seemed to me like that would be the case, but WHY?
Edwin
|
|
|