SOLUTION: Find the area of the shaded region. https://ibb.co/bjxZQDbF

We want to know the area of the two segments marked "XXX" below



The triangle is inscribed in a semicircle, i.e., its hypotenuse is a diameter,
so we know it is a right triangle.

Since it has a 30o angle, we know it is a 30-60-90 right triangle.

We know that the longer leg is 

You should learn the following information about the special 30-60-90
special right triangle.  It occurs very often.

The sides of the standard 30-60-90 right triangle:
The shorter leg is 1 unit long. 
The longer leg is  units long.
The hypotenuse is 2 units long.

Let the shorter leg of your 30-60-90 right triangle be x.

You are given the longer leg of the 30-60-90 triangle as 

So make the proportion:





cross-multiply:







So the shorter leg of the 30-60-90 special right triangle is 9 cm.

Therefore the area of the 30-60-90 special right triangle is


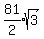 cm2

To get the area of the two segments marked XXX, we must find the radius
of the circle.  Since the hypotenuse is twice the shorter side, the
hypotenuse is (9)(2) = 18 cm. The hypotenuse is a diameter, so the radius is
half that or 9.

The area of the whole circle = 
The area of the semicircle the triangle is inscribed in is half that, or


So we subtract the area of the triangle from the area of the semicircle
and get

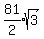 cm2

Factor out ,

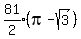 cm2, about 57.1 cm2
 
Edwin