|
Question 1209952: The function f(n) is defined for all integers n, such that
f(x) + f(y) = f(x + y) - 4xy - 1 + f(x^2) + f(y^2)
for all integers x and y, and f(1) = 1. Find f(n).
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! We are given the functional equation:
\[
f(x) + f(y) = f(x + y) - 4xy - 1 + f(x^2) + f(y^2)
\]
for all integers \( x, y \), along with the initial condition \( f(1) = 1 \). Our goal is to determine \( f(n) \) explicitly.
### Step 1: Plugging in \( x = 0, y = 0 \)
Substituting \( x = 0, y = 0 \) into the given equation:
\[
f(0) + f(0) = f(0) - 4(0)(0) - 1 + f(0^2) + f(0^2)
\]
Since \( f(0^2) = f(0) \), we simplify:
\[
2f(0) = f(0) - 1 + 2f(0)
\]
Canceling \( 2f(0) \) from both sides, we get:
\[
0 = -1 \Rightarrow f(0) = 0.
\]
### Step 2: Plugging in \( y = 1 \)
Setting \( y = 1 \) in the functional equation:
\[
f(x) + f(1) = f(x + 1) - 4x(1) - 1 + f(x^2) + f(1^2).
\]
Since \( f(1) = 1 \) and \( f(1^2) = f(1) = 1 \), we substitute:
\[
f(x) + 1 = f(x + 1) - 4x - 1 + f(x^2) + 1.
\]
Simplify:
\[
f(x) = f(x + 1) - 4x + f(x^2).
\]
### Step 3: Plugging in \( x = 1, y = 1 \)
Setting \( x = y = 1 \):
\[
f(1) + f(1) = f(2) - 4(1)(1) - 1 + f(1^2) + f(1^2).
\]
Using \( f(1) = 1 \):
\[
1 + 1 = f(2) - 4 - 1 + 1 + 1.
\]
\[
2 = f(2) - 3.
\]
\[
f(2) = 5.
\]
### Step 4: Plugging in \( x = 2, y = 1 \)
\[
f(2) + f(1) = f(3) - 4(2)(1) - 1 + f(2^2) + f(1^2).
\]
Using \( f(2) = 5 \), \( f(1) = 1 \), \( f(1^2) = 1 \):
\[
5 + 1 = f(3) - 8 - 1 + f(4) + 1.
\]
\[
6 = f(3) - 8 + f(4) + 1.
\]
\[
5 = f(3) - 8 + f(4).
\]
Rearrange:
\[
f(3) + f(4) = 13.
\]
### Step 5: Identifying a Pattern
Based on observed values \( f(1) = 1 \), \( f(2) = 5 \), and the recurrence relation, we suspect \( f(n) \) follows a quadratic pattern. Assume:
\[
f(n) = an^2 + bn + c.
\]
Using \( f(1) = 1 \):
\[
a(1)^2 + b(1) + c = 1 \Rightarrow a + b + c = 1.
\]
Using \( f(2) = 5 \):
\[
a(2)^2 + b(2) + c = 5 \Rightarrow 4a + 2b + c = 5.
\]
Using \( f(0) = 0 \):
\[
a(0)^2 + b(0) + c = 0 \Rightarrow c = 0.
\]
So,
\[
a + b = 1, \quad 4a + 2b = 5.
\]
Solving for \( a, b \):
\[
b = 1 - a,
\]
\[
4a + 2(1 - a) = 5.
\]
\[
4a + 2 - 2a = 5.
\]
\[
2a = 3.
\]
\[
a = \frac{3}{2}, \quad b = 1 - \frac{3}{2} = -\frac{1}{2}.
\]
Thus,
\[
f(n) = \frac{3}{2} n^2 - \frac{1}{2} n.
\]
Verifying,
\[
f(n) = \frac{3}{2} n(n - 1).
\]
Final Answer:
\[
\boxed{f(n) = \frac{3}{2} n(n-1).}
\]
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The function f(n) is defined for all integers n, such that
f(x) + f(y) = f(x + y) - 4xy - 1 + f(x^2) + f(y^2)
for all integers x and y, and f(1) = 1. Find f(n).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill, giving the answer f(n) = 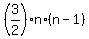 , is INCORRECT. , is INCORRECT.
I will show it below in this my post.
(a) Substitute x=0, y=0 into the basic formula. You will get
f(0) + f(0) = f(0) - 0 - 1 + f(0) + f(0).
Cancel f(0) in both sides everywhere where possible. You will get
0 = f(0) - 1
f(0) = 1.
(b) Substitute y=0 into the basic formula. Now x is an arbitrary integer number.
f(x) + f(0) = f(x+0) - 0 - 1 + f(x^2) + f(0),
f(x) + 1 = f(x) - 0 - 1 + f(x^2) + 1,
1 = f(x^2).
Thus, from the general basic formula, f(n^2) = 1 for any integer 'n'.
But it is not so from the formula f(n) = 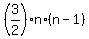 by @CPhill. by @CPhill.
It disproves and kills the solution by @CPhill to the death.
Let's go further in analyzing the problem.
In the general equation, replace the terms f(x^2) and f(y^2) by 1, as we deduced it above.
You will get
f(x) + f(y) = f(x+y) - 4xy + 1.
Put y= 1 in this equation
f(x) + f(1) = f(x+1) - 4x + 1,
f(x) + 1 = f(x+1) - 4x + 1,
f(x+1) = f(x) + 4x.
We get a nice recurrent formula and can calculate the values f(x) moving forward.
We get
f(2) = f(1) + 4*1 = 1 + 4 = 5;
f(3) = f(2) + 4*2 = 5 + 8 = 13;
f(4) = f(3) + 4*3 = 13 + 12 = 25.
But this equality f(4) = 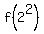 = 25 CONTRADICTS to equality f(n^2) = 1, which we established earlier above.
It tells that the given general formula DOES NOT define a function f. = 25 CONTRADICTS to equality f(n^2) = 1, which we established earlier above.
It tells that the given general formula DOES NOT define a function f.
So, the posted problem is SELF-CONTRADICTORY.
Its description DECEIVES the reader from the very beginning,
saying that this general formula defines a function.
On CONTRARY, it DOES NOT define.
In the last several days, I saw several similar ABSOLUTELY DEFECTIVE " problems ", submitted to the forum.
They all are created by unprofessional/(illiterate ?) Math composers.
|
|
|
| |