Question 1209926: (a) Let x, y, and z be positive real numbers. Find the largest possible value of
\sqrt{\frac{3x + 5y + 2z}{6x + 5y + 4z}} + \sqrt{\frac{2x + 5y + z}{6x + 5y + 5z}} + \sqrt{\frac{9x + y + 4z}{6x + 5y + 4z}}.
(b) Find \frac{z}{x} if (x,y,z) is a triple that gives the maximum value in Part (a).
Found 3 solutions by Edwin McCravy, ikleyn, mccravyedwin:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(a) Let x, y, and z be positive real numbers. Find the largest possible value of
\sqrt{\frac{3x + 5y + 2z}{6x + 5y + 4z}} + \sqrt{\frac{2x + 5y + z}{6x + 5y + 5z}} + \sqrt{\frac{9x + y + 4z}{6x + 5y + 4z}}.
(b) Find \frac{z}{x} if (x,y,z) is a triple that gives the maximum value in Part (a).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by Edwin (as Edwin McCravy) is incorrect.
It becomes incorrect starting from Edwin's assumption that x = y = z provide the maximum.
Edwin refers to the fact that "the arithmetic mean of expressions for non-negative numbers
always exceeds the geometric mean except when they are all the same".
This fact is true, but it has nothing in common with the assumption x = y = z.
This fact only means that the three expressions under the square roots should be equal,
but this does not implies or is equivalent to x = y = z.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
In his post as @mccravyedwin, Edwin writes
"It doesn't seem obvious to Ikleyn why it works just to substitute x = y = z = 1."
In response, I will say that
It doesn't seem obvious to  why it why it   work just to substitute x = y = z = 1.
To prove it, I will take x = y = 1, z = 0. In other words, I will assume that x and y both go to infinity
with the same rate, while z remains limited.
Then the expression work just to substitute x = y = z = 1.
To prove it, I will take x = y = 1, z = 0. In other words, I will assume that x and y both go to infinity
with the same rate, while z remains limited.
Then the expression
 will approach to
will approach to
 = = 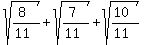 = 2.60398949 approximately, which is = 2.60398949 approximately, which is  than Edwin's number 2.489695145. than Edwin's number 2.489695145.
So, Edwin's invectives to my address have no any solid base.
Answer by mccravyedwin(406)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It doesn't seem obvious to Ikleyn why it works just to substitute x = y = z = 1.
Let's forget the means of x,y,z,w. I was thinking of that to get a starting
place to start my thinking from.
(a) Let x, y, and z be positive real numbers. Find the largest possible value of
 To me, it seems obvious that if all three variables approach infinity at the
same rate, they will approach
To me, it seems obvious that if all three variables approach infinity at the
same rate, they will approach
  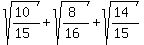  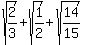  2.489695145 approximately, and that the value could not be higher than that,
Notice that is the same value as substituting 1 for all the variables. I am not
saying that proves anything, just that it starts us to thinking in the right
direction. I still think it's right. Maybe we could show it rigorously with
multivariable calculus by setting the partial derivatives equal zero, and
examining the behavior at that point.
(b) Find
2.489695145 approximately, and that the value could not be higher than that,
Notice that is the same value as substituting 1 for all the variables. I am not
saying that proves anything, just that it starts us to thinking in the right
direction. I still think it's right. Maybe we could show it rigorously with
multivariable calculus by setting the partial derivatives equal zero, and
examining the behavior at that point.
(b) Find  if (x,y,z) is a triple that gives the maximum value in Part
(a).
Since (1,1,1) is such a triple if (x,y,z) is a triple that gives the maximum value in Part
(a).
Since (1,1,1) is such a triple  .
Edwin .
Edwin
|
|
|