Question 1209923: Let x, y, and z be real numbers. If x^2 + y^2 + z^2 = 1, then find the maximum value of
3x + 4y + 5z + x^3 + \frac{4x^2*y)/{z} + \frac{z^5}{xy^2}
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Let f(x,y,z)=3x+4y+5z+x
3
+
z
4x
2
y
+
xy
2
z
5
and g(x,y,z)=x
2
+y
2
+z
2
−1=0.
We use the method of Lagrange multipliers to find the maximum value of f(x,y,z) subject to the constraint g(x,y,z)=0.
We need to solve the system of equations:
∇f=λ∇g
g(x,y,z)=0
First, let's find the gradients:
∇f=(3+3x
2
+
z
8xy
−
x
2
y
2
z
5
,4+
z
4x
2
−
xy
3
2z
5
,5−
z
2
4x
2
y
+
xy
2
5z
4
)
∇g=(2x,2y,2z)
Now, we set ∇f=λ∇g:
3+3x
2
+
z
8xy
−
x
2
y
2
z
5
=2λx
4+
z
4x
2
−
xy
3
2z
5
=2λy
5−
z
2
4x
2
y
+
xy
2
5z
4
=2λz
x
2
+y
2
+z
2
=1
This system of equations is highly nonlinear and difficult to solve analytically. However, we can make some observations.
If we consider the case where x,y,z>0, we have:
When x=0.6, y=0.8, and z is a small positive number, the term
z
4x
2
y
becomes very large.
When x,y are small positive numbers and z is close to 1, the term
xy
2
z
5
becomes very large.
This suggests that the maximum value might occur when x,y,z are all positive and have a certain relationship.
That's the only answer I can give for now!
Answer by ikleyn(52794)  (Show Source):
You can put this solution on YOUR website! .
Let x, y, and z be real numbers. If x^2 + y^2 + z^2 = 1, then find the maximum value of
3x + 4y + 5z + x^3 +  +  .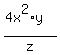
~~~~~~~~~~~~~~~~~~~~~~~~~~~
@CPhill finds it difficult to give a definitive answer in his post.
Meanwhile, the answer to this question is very simple: under given conditions,
the given function/expression has NO maximum.
It is because the term 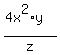of the expression has variable z in the denominator.
Take (x,y,z) in vicinity of ( ,, ), so that x^2 + y^2 + z^2 = 1 is valid,
and let z goes to zero from the positive side.
Then the term 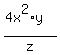tends to positive infinity,
and with this term, the whole expression tends to positive infinity.
////////////////////////////////
So the answer in the post by @CPhill is empty.
|
|
|
