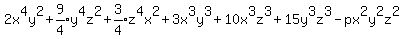SOLUTION: Find the maximum p such that 2x^4 y^2 + \frac{9}{4} y^4 z^2 + \frac{3}{4} z^4 x^2 + 3x^3 y^3 + 10x^3 z^3 + 15y^3 z^3 - px^2 y^2 z^2 is always nonnegative for all real x, y, and z

Let's substitute x=y=z=1 to see what p must be in that extreme case







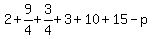
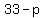
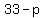
So for that case the maximum value for p would be 33.  But that doesn't prove it
by any means.  But it makes us suspect that might be the answer. Let's separate
the terms with only even exponents from those with only odd exponents. 



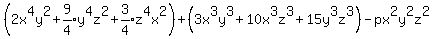Let A = 
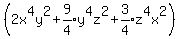Let B = 
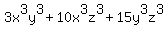Let C = 

A is always non-negative no matter what values x, y, and z take on.  Also it
has the largest exponents of variables. As the values of |x|, |y|, and |z| grow
larger and larger away from 1, the 4th power terms of A grow much faster than
the 3rd and 2nd power terms of B and C. 

So as the variables x, y, and z grow larger in absolute value, A is going to be
much more positive than B can ever be negative. 

So A+B will be positive for all values of variable of |x|, |y|, and |z| above 1.

And 
is always going to have the sign of p.
  
So I think that p = 33 (the case when x=y=z=1 will take care of all values of
x, y, and z.  

I agree this is not a formal proof.  But I think it's right.

Edwin