|
Question 1209876: Find the largest value of x where the plots of
f(x) = - \frac{2x + 5}{x + 3} and g(x) = \frac{12}{x - 1}
intersect.
Found 4 solutions by CPhill, ikleyn, greenestamps, Edwin McCravy:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! To find the intersection points of $f(x)$ and $g(x)$, we set $f(x) = g(x)$:
$$ - \frac{2x + 5}{x + 3} = \frac{12}{x - 1} $$
Multiply both sides by $(x + 3)(x - 1)$ to eliminate the denominators:
$$ -(2x + 5)(x - 1) = 12(x + 3) $$
$$ -(2x^2 - 2x + 5x - 5) = 12x + 36 $$
$$ -(2x^2 + 3x - 5) = 12x + 36 $$
$$ -2x^2 - 3x + 5 = 12x + 36 $$
$$ 0 = 2x^2 + 15x + 31 $$
Now, we use the quadratic formula to solve for $x$:
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
In this case, $a = 2$, $b = 15$, and $c = 31$.
$$ x = \frac{-15 \pm \sqrt{15^2 - 4(2)(31)}}{2(2)} $$
$$ x = \frac{-15 \pm \sqrt{255 - 248}}{4} $$
$$ x = \frac{-15 \pm \sqrt{7}}{4} $$
We have two solutions:
$$ x_1 = \frac{-15 + \sqrt{7}}{4} $$
$$ x_2 = \frac{-15 - \sqrt{7}}{4} $$
We want to find the largest value of $x$, so we choose the solution with the plus sign:
$$ x_1 = \frac{-15 + \sqrt{7}}{4} $$
We approximate the value of $\sqrt{7} \approx 2.646$.
$$ x_1 \approx \frac{-15 + 2.646}{4} \approx \frac{-12.354}{4} \approx -3.0885 $$
$$ x_2 \approx \frac{-15 - 2.646}{4} \approx \frac{-17.646}{4} \approx -4.4115 $$
Therefore, the largest value of $x$ is:
$$ x = \frac{-15 + \sqrt{7}}{4} $$
Final Answer: The final answer is $\boxed{\frac{-15 + \sqrt{7}}{4}}$
Answer by ikleyn(52803)  (Show Source):
You can put this solution on YOUR website! .
Polynomials-and-rational-expressions/1209876: Find the largest value of x where the plots of
f(x) = - \frac{2x + 5}{x + 3} and g(x) = \frac{12}{x - 1}
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Be aware !
The answer in the post by @CPhill is incorrect.
He made an arithmetic error while calculated the discriminant of the quadratic equation.
The discriminant is NEGATIVE, which means that the quadratic equation does not have real solutions.
The answer is that the plots of these given functions do not intersect in real domain.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solutions are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
///////////////////////////////////////////////
In his post, @greenestamps presented a result, different from mine.
It is because, by mistake, he solved DIFFERENT equation than it is given in the original post.
In the original post, the equations/functions were
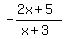f(x) =  and g(x) =  .
In his post, @greenestamps mistakenly used functions
f(x) =  and g(x) = .
Notice that his function f(x) has the opposite sign, comparing with the given function f(x).
Therefore, it is no wonder that he came to different answer, comparing with mine.
Thus my conclusion remains unchangeable:
******************************************************************
the solution and the answer in the post by @CPhill both are incorrect.
******************************************************************
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
In the post by Edwin, he made the same error, which @greenestamps made in his post.
Edwin plotted function f(x) = 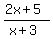 , while in the original problem the given function is with the opposite sign f(x) =  .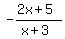
So, it is not wonder that using wrong function, Edwin got wrong answer.
For your convenience, I prepared the plot of the given functions. It is shown under this link
https://www.desmos.com/calculator/dog5dqdqlc
https://www.desmos.com/calculator/dog5dqdqlc
In addition to my algebraic explanations in my post above, this plot clearly shows visually
that there no any intersection/intersections between the plots of the given functions.
Answer by greenestamps(13200)  (Show Source):
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
On your TI-84 graphing calculator,
1. Press Y=
2. Make the screen read:
Plot1 Plot2 Plot3
/Y1 =(2X+5)/(X+3)
/Y2 =12/(X-1)
3. Press ZOOM then 6
See this graph:
Notice there are two points where the curves intersect. I have
drawn circles around the two points. We want the x-coordinate
of the circled point on the right for it will have a larger
x-value.
4. Press 2ND TRACE 5
Use the right arrow key to move the cursor to the right as close
as possible to the point.
5. Press ENTER ENTER ENTER.
Read X=7.3059371 at the bottom of the screen.
That's the approximate answer.
Edwin
|
|
|
| |
