SOLUTION: You want to be able to withdraw $45,000 from your account each year for 15 years after you retire. You expect to retire in 25 years. If your account earns 4% interest, how mu

Algebra ->  Finance -> SOLUTION: You want to be able to withdraw $45,000 from your account each year for 15 years after you retire. You expect to retire in 25 years. If your account earns 4% interest, how mu      Log On


   

Question 1209866: You want to be able to withdraw $45,000 from your account each year for 15 years after you retire.
You expect to retire in 25 years.
If your account earns 4% interest, how much will you need to deposit each year until retirement to achieve your retirement goals?
Answer by ikleyn(52814) About Me  (Show Source):
You can put this solution on YOUR website!
.
You want to be able to withdraw $45,000 from your account each year for 15 years after you retire.
You expect to retire in 25 years.
If your account earns 4% interest, how much will you need to deposit each year until retirement to achieve your retirement goals?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~


            I will solve this problem in two steps.

                            Step  1. 

First, let's determine how much money X should be accumulated on the account during 25 years when you make your annual deposits,
in order for to have enough to withdraw $45,000 each year for 15 years of your retirement.


Withdrawing $45,000 each year, your account (the remaining money) still earns 4% per annum compounded at the end of each year.   
So, during this period of 15 years, the annuity works as a sinking fund.


If you withdraw at the beginning of each year for living, the formula for the starting value  X  of sinking fund is

    X = 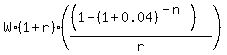W%2A%281%2Br%29%2A%28%28%281-%281%2B0.04%29%5E%28-n%29%29%29%2Fr%29,     (1)


where W is the annual withdraw amount; r is the annual rate of compounding as the decimal,
and n is the number of withdrawals.


In this problem,  W = $45,000,  r = 0.04;  n = 15.  Substitute these values into the formula (1) and calculate X

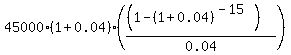    X = 45000%2A%281%2B0.04%29%2A%28%28%281-%281%2B0.04%29%5E%28-15%29%29%29%2F0.04%29 = $520340.53.     (2)


So, after 25 years of accumulating money, the fund should have $520340.53.


Thus, the first step of calculations is complete.

                            Step  2. 

Now we are in position to determine how much should be deposited each year during 25 years when you make annual deposits.


I will assume that the annual deposits are made at the end of each of 25 years.


Then the fund works as a standard Ordinary Annuity saving plan.
So, we use this formula for the future value

    FV = 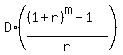D%2A%28%28%281%2Br%29%5Em-1%29%2Fr%29,     (3)


where D is the annual deposit amount; r is the annual rate of compounding as the decimal,
and m is the number of deposits.


In this problem,  FV = $500327.43 as we determined above;  D is the unknown value of the deposit to find from the equation; 
r = 0.04;  m = 25.  Substitute these values into the formula (3) 

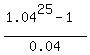    520340.53 = D%2A%28%281.04%5E25-1%29%2F0.04%29.     (4)


The multiplier  %281.04%5E25-1%29%2F0.04  is  41.64591,  


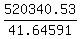It implies from equation (4)  that  D = 520340.53%2F41.64591 = $12494.40.


It is your ANSWER:  During 25 years of the accumulating period you should deposit $12494.40 at the end of each year to your account.

                    Then you will be able to withdraw $45000 at the beginning of every year during 15 years.


For clarity, notice that in 25 years, you deposit in the bank 25*12494.40 = 312360 dollars.


During following 15 years, you withdraw from the bank 15*45000 = 675000  dollars.


The difference 675000 - 312360 = 362640 dollars is the interest, which your account earned 
during 25 + 15 = 40 years.

Solved.