Question 1209850: Given that log_{4n} 40 sqrt(3) = log_{2n} 10, find n^4.
Answer by ikleyn(52817)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given that log_{4n} 40 sqrt(3) = log_{2n} 10, find n^4.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
You are given
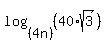 = = 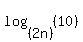 . (1)
Let x be the common numerical value of each side of (1), so we can write . (1)
Let x be the common numerical value of each side of (1), so we can write
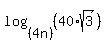 = x, (2) = x, (2)
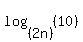 = x. (3)
Then we can rewrite (2) and (3) in this form, respectively = x. (3)
Then we can rewrite (2) and (3) in this form, respectively
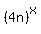 = = 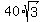 , (2') , (2')
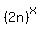 = 10. (3')
Divide equation (2') by equation (3'). You will get = 10. (3')
Divide equation (2') by equation (3'). You will get
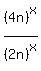 = = 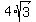 .
You can simplify left side .
You can simplify left side
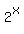 = = 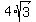 .
Hence,
x = .
Hence,
x = 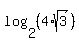 .
At this point, we solved half of the problem
and have found the numerical value of each
expression in the left side of equations (2) and (3).
Now we are going to make next step and to find n and .
At this point, we solved half of the problem
and have found the numerical value of each
expression in the left side of equations (2) and (3).
Now we are going to make next step and to find n and 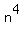 .
We can write equation (3) in the form .
We can write equation (3) in the form
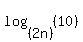 = = 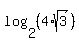 . (4)
Let y be the common numerical value of each side of (4), so we can write . (4)
Let y be the common numerical value of each side of (4), so we can write
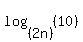 = y, (5) = y, (5)
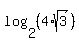 = y. (6)
Then we can rewrite (5) and (6) in this form, respectively = y. (6)
Then we can rewrite (5) and (6) in this form, respectively
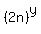 = 10, (5') = 10, (5')
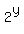 = = 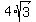 . (6')
Divide equation (5') by equation (6'). You will get . (6')
Divide equation (5') by equation (6'). You will get
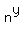 = = 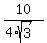 = = 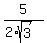 = = 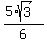 .
Take logarithm of both sides
y*log(n) = .
Take logarithm of both sides
y*log(n) = 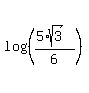 . (7)
In this formula, it does not matter, which base of logarithm I use.
Let's the base of logarithm in this equation be 10.
From equation (7),
log(n) = . (7)
In this formula, it does not matter, which base of logarithm I use.
Let's the base of logarithm in this equation be 10.
From equation (7),
log(n) = 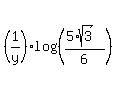 .
We can substitute here expression (6) for y. We get then
log(n) = .
We can substitute here expression (6) for y. We get then
log(n) = 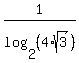 * * 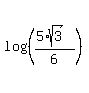 .
This is the "precise" expression for log(n).
We can find its numerical value
log(n) = .
This is the "precise" expression for log(n).
We can find its numerical value
log(n) = 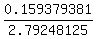 = 0.057074.
Hence, n = = 0.057074.
Hence, n = 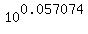 = 1.140444, and = 1.140444, and 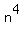 = = 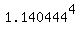 = 1.691601, approximately.
At this point, the solution is complete and the value of = 1.691601, approximately.
At this point, the solution is complete and the value of 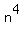 is found.
ANSWER. is found.
ANSWER. 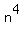 = = 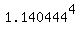 = 1.691601, approximately. = 1.691601, approximately.
Solved.
After completing this solution, I checked equation (1)
and found that both sides are equal at n = 1.140444.
|
|
|