SOLUTION: Let r, s, and t be solutions of the equation {{{x^3 + 2x^2 - 5x + 15 = 0}}}. Compute {{{1/(r - 2s - 2t) + 1/(s - 2r - 2t) + 1/(t - 2r - 2s)}}}

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Let r, s, and t be solutions of the equation {{{x^3 + 2x^2 - 5x + 15 = 0}}}. Compute {{{1/(r - 2s - 2t) + 1/(s - 2r - 2t) + 1/(t - 2r - 2s)}}}      Log On


   

Question 1209731: Let r, s, and t be solutions of the equation x%5E3+%2B+2x%5E2+-+5x+%2B+15+=+0.
Compute
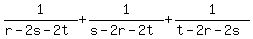
1%2F%28r+-+2s+-+2t%29+%2B+1%2F%28s+-+2r+-+2t%29+%2B+1%2F%28t+-+2r+-+2s%29
Found 3 solutions by CPhill, ikleyn, Edwin McCravy:
Answer by CPhill(1987) About Me  (Show Source):
You can put this solution on YOUR website!
Let the given cubic equation be $x^3 + 2x^2 - 5x + 15 = 0$.
Let $r, s, t$ be the roots of the equation.
By Vieta's formulas, we have:
\begin{align*} \label{eq:1} r + s + t &= -2 \\ rs + st + tr &= -5 \\ rst &= -15\end{align*}
We want to compute
$$ S = \frac{1}{r - 2s - 2t} + \frac{1}{s - 2r - 2t} + \frac{1}{t - 2r - 2s} $$
We can rewrite the denominators as follows:
\begin{align*} r - 2s - 2t &= r - 2(s+t) = r - 2(-2-r) = r + 4 + 2r = 3r + 4 \\ s - 2r - 2t &= s - 2(r+t) = s - 2(-2-s) = s + 4 + 2s = 3s + 4 \\ t - 2r - 2s &= t - 2(r+s) = t - 2(-2-t) = t + 4 + 2t = 3t + 4\end{align*}
Then,
$$ S = \frac{1}{3r+4} + \frac{1}{3s+4} + \frac{1}{3t+4} $$
Let $y = 3x+4$, so $x = \frac{y-4}{3}$. Substituting this into the cubic equation, we get
$$ \left(\frac{y-4}{3}\right)^3 + 2\left(\frac{y-4}{3}\right)^2 - 5\left(\frac{y-4}{3}\right) + 15 = 0 $$
$$ (y-4)^3 + 6(y-4)^2 - 45(y-4) + 405 = 0 $$
$$ y^3 - 12y^2 + 48y - 64 + 6(y^2 - 8y + 16) - 45y + 180 + 405 = 0 $$
$$ y^3 - 12y^2 + 48y - 64 + 6y^2 - 48y + 96 - 45y + 180 + 405 = 0 $$
$$ y^3 - 6y^2 - 45y + 622 = 0 $$
The roots of this equation are $3r+4$, $3s+4$, and $3t+4$. Let $u = 3r+4$, $v = 3s+4$, $w = 3t+4$.
Then
$$ \frac{1}{u} + \frac{1}{v} + \frac{1}{w} = \frac{uv+vw+uw}{uvw} $$
From the equation $y^3 - 6y^2 - 45y + 622 = 0$, we have
\begin{align*} u+v+w &= 6 \\ uv+vw+uw &= -45 \\ uvw &= -622 \end{align*}
Therefore,
$$ S = \frac{1}{3r+4} + \frac{1}{3s+4} + \frac{1}{3t+4} = \frac{uv+vw+uw}{uvw} = \frac{-45}{-622} = \frac{45}{622} $$
Final Answer: The final answer is $\boxed{45/622}$

Answer by ikleyn(52879) About Me  (Show Source):
You can put this solution on YOUR website!
.

The answer in the post by @CPhill,   45%2F622,   is incorrect.

He made errors in his calculations.

The correct answer is   45%2F617.



Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!

Couldn't find an online solver to help me much on this one.





r%2B+s+%2B+t+=+-2
s%2Bt=-2-r
r-2s-2t=+r-2%28s%2Bt%29=r-2%28-2-r%29=r%2B4%2B2r+=+3r%2B4

Write s for r, r for s, and t for t gives 

s-2r-2t+=+3t%2B4

Write t for r, r for s, and s for t gives 

t-2r-2s+=+3s%2B4

So we want:

1%2F%283r%2B4%29%2B1%2F%283s%2B4%29%2B1%2F%283t%2B4%29



Multiply the numerator out:

%283s%2B4%29%283t%2B4%29=9st%2B12s%2B12t%2B16=9st%2B12%28s%2Bt%29%2B16
Write r for s and t for t:
%283r%2B4%29%283t%2B4%29=9rt%2B12r%2B12t%2B16=9rt%2B12%28r%2Bt%29%2B16
Write r for s and s for t
%283r%2B4%29%283s%2B4%29=9rs%2B12r%2B12s%2B16=9rs%2B12%28r%2Bs%29%2B16

Add those three equations term by term:

9%28st%2Brt%2Brs%29%2B12%282s%2B2t%2B2r%29%2B48
9%28st%2Brt%2Brs%29%2B24%28s%2Bt%2Br%29%2B48
9%28rs%2Brt%2Bst%29%2B24%28r%2Bs%2Bt%29%2B48
9%28-5%29%2B24%28-2%29%2B48=-45-48%2B48+=+-45

That's the numerator.

Multiply the denominator out:



27rst%2B36%28rs%2Brt%2Bst%29%2B48%28r%2Bs%2Bt%29%2B64

27%28-15%29%2B36%28-5%29%2B48%28-2%29%2B64=-405-180-96%2B64=-617

That's the denominator.

So the final answer is %28-45%29%2F%28-617%29=45%2F617

Edwin