SOLUTION: Suppose P(x) is a polynomial of smallest possible degree such that: * P(x) has rational coefficients. * P(-2) = P(\sqrt{5}) = P(\sqrt{7}) = P(\sqrt{17}) = 0. * P(-1) = 13. Dete

In this problem, a polynomial P(x) with rational coefficients has the roots
 
    -2, ,  ,  .


that are quadratic irrationalities.


To make a polynomial with rational coefficients, which has these roots, we shall
associate the conjugate number over Q with every quadratic irrationality.


So, P(x) has the form

    P(x) =  =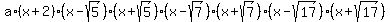 

         = .


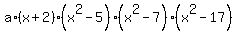Here "a" is the coefficient, now unknown.  We will determine it from the condition P(-1) = 13.
It gives

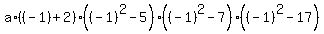            = 13,  

or

           a*1*(-4)*(-6)*(-16) = 13,

           a*(-384) = 13,

           a = .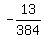


Now the polynomial is fully defined  P(x) = .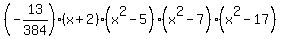


To find P(0), plug in 0 instead of x:  

    P(0) =  =  =  = .


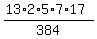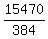ANSWER.  P(x) = 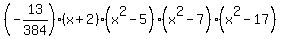  and  P(0) = .