|
Question 1209607: The domain of the function r(x) = (x^2 + 1)/(1 - x)^2 is (-infty,1) U (1,infty). What is the range?
Found 3 solutions by mccravyedwin, math_tutor2020, ikleyn:
Answer by mccravyedwin(409)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
r(x) = p/q
p = x^2+1
q = (1-x)^2
Apply derivatives
p' = 2x
q' = -2(1-x)
Then apply the quotient rule.
r'(x) = ( p'*q - p*q' )/( q^2 )
r'(x) = ( 2x*(1-x)^2 - (x^2+1)*(-2(1-x)) )/( ((1-x)^2)^2 )
r'(x) = ( 2x*(1-x)^2 + 2(x^2+1)*(1-x) )/( (1-x)^4 )
r'(x) = ( 2x*(1-2x+x^2) + 2(-x^3+x^2-x+1) )/( (1-x)^4 )
r'(x) = ( (2x-4x^2+2x^3) + (-2x^3+2x^2-2x+2) )/( (1-x)^4 )
r'(x) = (-2x^2 + 2)/( (1-x)^4 )
r'(x) = ( -2(x^2 - 1) )/( (1-x)^4 )
r'(x) = ( -2(x-1)(x+1) )/( (x-1)^4 )
r'(x) = ( -2(x+1) )/( (x-1)^3 )
Set the derivative equal to zero and solve for x.
r'(x) = 0
( -2(x+1) )/( (x-1)^3 ) = 0
-2(x+1) = 0
x+1 = 0
x = -1
A local min, local max, or saddle point occurs at x = -1.
Use either the first derivative test or second derivative test to determine that the local min occurs at x = -1.
I'll leave this for the student to do.
If x = -1, then,
r(x) = (x^2+1)/( (1-x)^2 )
r(-1) = ((-1)^2+1)/( (1-(-1))^2 )
r(-1) = (1+1)/( (1+1)^2 )
r(-1) = 2/4
r(-1) = 1/2
This is the smallest output possible.
Therefore the range is any real y value equal to 1/2 or larger.
You can use a graphing tool like Desmos or GeoGebra to confirm.

Note that as x heads to either positive or negative infinity, the curve approaches the horizontal asymptote y = 1. This is because we have x^2 up top over x^2 down below (after expanding). So we basically have  We only worry about the leading terms when x gets really large. We only worry about the leading terms when x gets really large.
--------------------------------------------------------------------------
--------------------------------------------------------------------------
Answer: The range is [1/2, infinity)
The square bracket includes the endpoint.
Answer by ikleyn(52914)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The domain of the function r(x) = (x^2 + 1)/(1 - x)^2 is (-infty,1) U (1,infty). What is the range?
~~~~~~~~~~~~~~~~~~~~~~~~~
I will provide another solution, which uses Algebra only
and does not use Calculus.
Real number "t" belongs to the range of this function if and only if
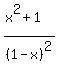 = t for some real x. (1)
Rewrite (1) in an equivalent form = t for some real x. (1)
Rewrite (1) in an equivalent form
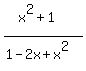 = t, = t,
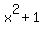 = = 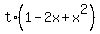 ,
x^2 + 1 = tx^2 - 2tx + t,
(1-t)x^2 + 2tx + (1-t) = 0.
This last quadratic equation has a real solution IF and ONLY IF the discriminant is non-negative
d = b^2 - 4ac >= 0,
or
(2t)^2 - 4*(1-t)*(1-t) >= 0,
4t^2 - 4*(1-t)^2 >= 0,
t^2 - 1 + 2t - t^2 >=0,
2t >= 1,
t >= 1/2.
At this point, the solution is complete.
ANSWER. The domain is the set of all real numbers greater than or equal to 1/2. ,
x^2 + 1 = tx^2 - 2tx + t,
(1-t)x^2 + 2tx + (1-t) = 0.
This last quadratic equation has a real solution IF and ONLY IF the discriminant is non-negative
d = b^2 - 4ac >= 0,
or
(2t)^2 - 4*(1-t)*(1-t) >= 0,
4t^2 - 4*(1-t)^2 >= 0,
t^2 - 1 + 2t - t^2 >=0,
2t >= 1,
t >= 1/2.
At this point, the solution is complete.
ANSWER. The domain is the set of all real numbers greater than or equal to 1/2.
Solved.
---------------------------
The solution and the answer in the post by Edwin are incorrect.
|
|
|
| |