Question 1209566: Please help. Thank you in advance.
Given tan рќ›ј =7/24, рќ›ј in the third quadrant, sin рќ›Ѕ =2/в€љ13, рќ›Ѕ in the second quadrant, find:
a) the quadrant containing рќ›ј + рќ›Ѕ
b) the quadrant containing рќ›ј - рќ›Ѕ
Answer by ikleyn(52834)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Please help. Thank you in advance.
Given tan рќ›ј =7/24, рќ›ј in the third quadrant, sin рќ›Ѕ =2/в€љ13, рќ›Ѕ in the second quadrant, find:
a) the quadrant containing рќ›ј + рќ›Ѕ
b) the quadrant containing рќ›ј - рќ›Ѕ
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Notice that 7^2 + 24^ = 625 = 25^2.
So, you may think that
tan(a) =  in the third quadrant is in the third quadrant is 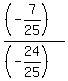 = =  .
In other words, you may think that sin(a) = .
In other words, you may think that sin(a) = 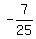 , cos(a) = , cos(a) = 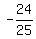 .
The signs at sin(a) and cos(a) do agree that "a" is in the third quadrant.
Next, you are given that sin(b) = .
The signs at sin(a) and cos(a) do agree that "a" is in the third quadrant.
Next, you are given that sin(b) = 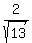 in the second quadrant; so, you can calculate
cos(b) = in the second quadrant; so, you can calculate
cos(b) = 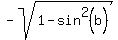 = = 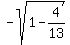 = = 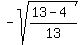 = = 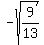 = =  .
The sign at cos(b) does agree that "b" is in the second quadrant.
Now, as you know sin(a) .
The sign at cos(b) does agree that "b" is in the second quadrant.
Now, as you know sin(a) 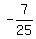 , cos(a) = , cos(a) = 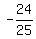 , sin(b) = , sin(b) = 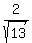 , cos(b) = , cos(b) =  , you can calculate
sin(a+b) = sin(a)*cos(b) + cos(a)*sin(b) = , you can calculate
sin(a+b) = sin(a)*cos(b) + cos(a)*sin(b) = 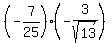 + +  = = 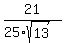 - - 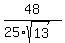 =
= =
= 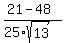 = = 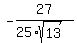 ,
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b) = ,
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b) = 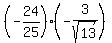 - - 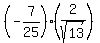 = = 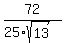 - - 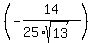 =
= =
=  = = 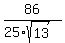 .
Thus, sin(a+b) is a negative real number; cos(a+b) is a positive real number.
It means that angle a+b is in fourth quadrant.
ANSWER. Angle a+b is in fourth quadrant. .
Thus, sin(a+b) is a negative real number; cos(a+b) is a positive real number.
It means that angle a+b is in fourth quadrant.
ANSWER. Angle a+b is in fourth quadrant.
Part (a) is solved completely.
For part (b), calculate sin(a-b) and cos(a-b) similarly; then make a conclusion about angle a-b.
You just have a TEMPLATE for it.
|
|
|