Question 1209515: Hi
There were some oranges in baskets A B and C. The ratio of A to B and C is 1 to 4. The ratio of C to A and B is 3 to 4. How many oranges were in C if there were 54 more oranges in B than in A.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1987)   (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem:
1. **Express the ratios as fractions:**
* A : B : C = 1 : 3 can be written as A/B = 1/3
* C : (A + B) = 3 : 4 can be written as C/(A + B) = 3/4
2. **Express B in terms of A:**
From A/B = 1/3, we get B = 3A
3. **Substitute B in the second ratio:**
C / (A + 3A) = 3/4
C / 4A = 3/4
4. **Express C in terms of A:**
C = (3/4) * 4A
C = 3A
5. **Use the information about the difference between A and B:**
B = A + 50
Since B = 3A, we can write:
3A = A + 50
2A = 50
A = 25
6. **Find the number of oranges in C:**
C = 3A
C = 3 * 25
C = 75
Therefore, there were 75 oranges in basket C.
Answer by ikleyn(52851)  (Show Source):
You can put this solution on YOUR website! .
There were some oranges in baskets A, B, and C.
The ratio of A to B and C is 1 to 4.
The ratio of C to A and B is 3 to 4.
How many oranges were in C if there were 54 more oranges in B than in A.
~~~~~~~~~~~~~~~~~~~~~~~
Tutor @CPhill reads and interprets the problem incorrectly -
and therefore, as a consequence, his solution and his answer are incorrect.
Below is my correct solution.
From the problem, we have this equation
 =  ,
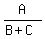which implies
4A = B + C.
From the problem, we also have this equation
 =  ,
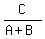which implies
4C = 3A + 3B.
So, we have these three equations
4A = B + C, (1)
4C = 3A + 3B, (2)
B - A = 54. (3)
You may write equations in standard matrix form and solve by Gauss-Jordan elimination.
You may use manual solution or some technique, like your regular calculator or online calculator
to save your time and avoid routine job.
I used online calculator wwww.reshish.com
It provides the solution A = 63, B = 117, C = 135
and also the steps, if you need them.
In any case, the ANSWER for C is C = 135 oranges.
I checked this answer manually by substituting the values of A, B and C into equations (1), (2) and (3)
and found that the solution is valid.
Solved.
Ignore the solution by @CPhill and his answer, since they both are incorrect/irrelevant/inadequate.
|
|
|
