SOLUTION: Find the range of values of k for which the expression x^2 + kx + (k+3) is positive for all real values of x. Hence, fine the range of values of x for which (2x-1)(3-x)/x^2+4x+7 <

                Part (a)


Consider the discriminant of the quadratic polynomial x^2 + kx + (k+3).


The discriminant is  d = b^2 - 4ac = k^2 - 4*(k+3) = k^2 - 4k - 12 = (k-6)*(k+2).


We see that the discriminant is negative in the interval -2 < k < 6.

It means that the polynomial does not have real zeroes if -2 < k < 6.
  
From the other side hand, its leading coefficient at x^2, "1", is positive. 
It means that the polynomial  x^2 + kx + (k+3) is always positive, for all real values of x,
if k is in the open interval (-2,6).


Thus, part (a) is solved/answered completely.



                Part (b)


Consider this rational function  .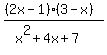


Its denominator is of the form x^2 + kx + (k+3) at k = 4.
We considered such polynomials in part (a) and proved that for k from the interval (-2,6) the polynomial is always positive,
for all real values of x.  The value of k= 4 is from this interval - so, the polynomial x^2 + 4x + 7 in the denominator
is always positive, for all real values of x.


Therefore, inequality 

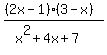     < 0     (1)

is equivalent to this simplified inequality

    (2x-1)*(3-x) < 0.    (2)


This inequality (2) has the leading coefficient -2 at x^2 and the roots 1/2 and 3,
so the left side is the downward parabola with x-intercepts 1/2 and 3.


So, the inequality (2) has the solution set   < x < 3.


It implies that inequality (1) has the same solution set   < x < 3.


Thus the range of values of x for which 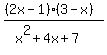  < 0  is  (,).    ANSWER


At this point, part (b) is solved completely.