.
Squares PQRS and PTUV both have an area of 256. Line segment PT lies on the diagonal PR of square PQRS. Find the length of WR.
Link to diagram: https://ibb.co/M95y0dm
~~~~~~~~~~~~~~~~~~~~
The squares have equal areas of 256 square units, each.
Hence, the squares are congruent and have the side size of 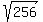 = 16 units, each.
Side PT lies on diagonal PR, which is
= 16 units, each.
Side PT lies on diagonal PR, which is 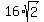 units long.
Hence and therefore, the segment WR has the length
units long.
Hence and therefore, the segment WR has the length
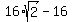 =
= 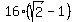 = 6.627416998 units (approximately).
Round it as you want.
= 6.627416998 units (approximately).
Round it as you want.
Solved.