Question 1209473: Evaluate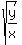 , where x and y are positive integers, and , where x and y are positive integers, and  . .
CC13F #8
Answer by ikleyn(52884)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Evaluate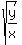 , where x and y are positive integers, and , where x and y are positive integers, and  . .
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
D U P L I C A T E
I solved this problem at this forum yesterday under this link
https://www.algebra.com/algebra/homework/expressions/expressions.faq.question.1209466.html
https://www.algebra.com/algebra/homework/expressions/expressions.faq.question.1209466.html
For your convenience, I copy-paste this solution here again.
S O L U T I O N
Your starting equation is
x^5 - x^3*y^3 = 12393, (1)
or
x^3*(x^2 - y^3) = 12393. (2)
Integer number 12393 has the primary decomposition 12393 = 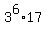 ,
so the last equation is
x^3*(x^2 - y^3) = ,
so the last equation is
x^3*(x^2 - y^3) = 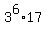 . (3)
From it, it is clear that for x, y to be integer solutions to this equation, it is necessary that x be 1, or 3, or 3^2 = 9.
So, we should consider these three cases.
(a) x = 1. Then from equation (3)
x^2 - y^3 = 3^6*17 = 12393, y^3 = 1 - 12393 = -12392.
But this number is not a positive perfect cube, so this way does not work.
(b) x = 3. Then from equation (3)
x^2 - y^3 = 3^3*17 = 459, y^3 = 9 - 459 = -450.
But this number is not a positive perfect cube, so this way does not work.
(c) x = 3^2 = 9. Then from equation (3)
x^2 - y^3 = 17, y^3 = 81 - 17 = 64.
This number, 64, is a positive perfect cube, so y = 4.
Thus, the solution to the given equation in this pair of positive integer numbers (x,y) = (3,4).
Then . (3)
From it, it is clear that for x, y to be integer solutions to this equation, it is necessary that x be 1, or 3, or 3^2 = 9.
So, we should consider these three cases.
(a) x = 1. Then from equation (3)
x^2 - y^3 = 3^6*17 = 12393, y^3 = 1 - 12393 = -12392.
But this number is not a positive perfect cube, so this way does not work.
(b) x = 3. Then from equation (3)
x^2 - y^3 = 3^3*17 = 459, y^3 = 9 - 459 = -450.
But this number is not a positive perfect cube, so this way does not work.
(c) x = 3^2 = 9. Then from equation (3)
x^2 - y^3 = 17, y^3 = 81 - 17 = 64.
This number, 64, is a positive perfect cube, so y = 4.
Thus, the solution to the given equation in this pair of positive integer numbers (x,y) = (3,4).
Then 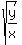 is this irrational number is this irrational number  = = 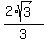 = 1.154700538 (rounded). ANSWER = 1.154700538 (rounded). ANSWER
Solved.
|
|
|