Question 1209472: Find the sum of the proper divisors of 1 825 346.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52832)   (Show Source):
You can put this solution on YOUR website! .
Find the sum of the proper divisors of 1 825 346.
~~~~~~~~~~~~~~~~~~~~~~~~~
Prime decomposition is 1825346 =  .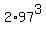
The proper divisors are 97, 97^2, 97^3, 2, 2*97, 2*97^2.
The sum of all proper divisors is
97 + 97^2 + 97^3 + 2 + 2*97 + 2*97^2 = 941193. ANSWER
-----------------------
@greenestamps noticed that 1 is also a proper divisor and should be included in the sum.
It is true, I missed it, sorry.
The correct sum of all proper divisors is
1 + 97 + 97^2 + 97^3 + 2 + 2*97 + 2*97^2 = 941194.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
After finding that the prime number decomposition of the given number is 2(97^3), you can find the sum of the proper divisors by listing them and adding, as the other tutor did.
Alternatively, you can find the answer by using a process that finds the sum of ALL the divisors and subtract the given number from that sum to find the sum of the proper divisors.
The sum of all the divisors of the number (2)(97^3) is
Then the sum of the proper divisors is 2766540-1825346 = 941194.
ANSWER: 941194
----------------------------------------------------------
Note the other tutor does not consider 1 to be a proper divisor, so her answer is 941193. I believe 1 is considered to be a proper divisor of any integer....
|
|
|
