SOLUTION: find all solutions: 3sin^2x+2sinx-1=0; in the interval [0,2pi)

Introduce new variable  u = sin(x).


Then your equation takes the form

    3u^2 + 2u - 1 = 0.


Factorize

    (3u-1)*(u+1) = 0.


Its roots are  u = 1/3  and  u= -1.


So, we consider now two cases


    (a)  sin(x) = 1/3,  which gives two solutions  x = 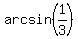  and  x =  - .


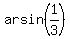    (b)  sin(x) = -1,   which gives the solution   x =   = .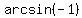


At this point, the problem is solved completely.


ANSWER.  The solutions to the given equation in the given interval are 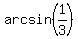 ,   -  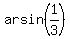 and  .